| Tridyakis icosahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 120, E = 180 V = 44 (χ = −16) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU 45 |
| dual polyhedron | Icositruncated dodecadodecahedron |
In geometry, the tridyakis icosahedron is the dual polyhedron of the nonconvex uniform polyhedron, icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.
The triangles have one angle of , one of and one of . The dihedral angle equals . Part of each triangle lies within the solid, hence is invisible in solid models.
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.
In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.
In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron. The net of the rhombic dodecahedral pyramid also shares the same topology.
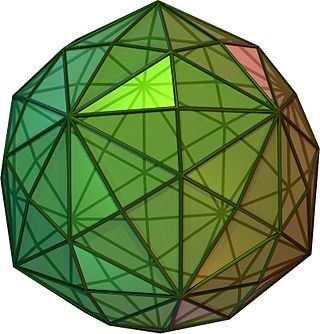
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron or kisrhombic triacontahedron is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.
In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.
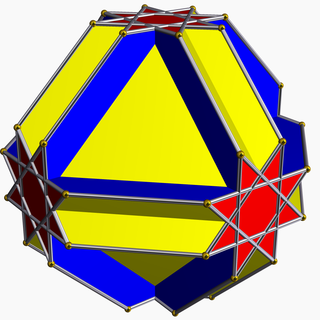
In geometry, the cubitruncated cuboctahedron or cuboctatruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16. It has 20 faces (8 hexagons, 6 octagons, and 6 octagrams), 72 edges, and 48 vertices,and has a shäfli symbol of tr{4,3/2}
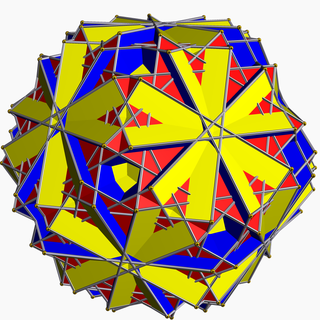
In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U68. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices. It is given a Schläfli symbol t0,1,2{5⁄3,3}, and Coxeter-Dynkin diagram, .
In geometry, the great snub icosidodecahedron is a nonconvex uniform polyhedron, indexed as U57. It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices. It can be represented by a Schläfli symbol sr{5⁄2,3}, and Coxeter-Dynkin diagram .
In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is a stellation of the rhombic triacontahedron, and can also be called small stellated triacontahedron. Its dual is the dodecadodecahedron.
In geometry, the great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron. It is the dual of the great icosidodecahedron (U54). Like the convex rhombic triacontahedron it has 30 rhombic faces, 60 edges and 32 vertices.
In geometry, the great triambic icosahedron and medial triambic icosahedron (or midly triambic icosahedron) are visually identical dual uniform polyhedra. The exterior surface also represents the De2f2 stellation of the icosahedron. These figures can be differentiated by marking which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas. Alternatively, if the faces are filled with the even–odd rule, the internal structure of both shapes will differ.
In geometry, the small stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great dodecahedron. It has 60 intersecting triangular faces.
In geometry, the medial deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the rhombidodecadodecahedron. Its 60 intersecting quadrilateral faces are kites.
In geometry, the great stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great icosahedron. It has 60 intersecting triangular faces.
In geometry, the great deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the nonconvex great rhombicosidodecahedron. It is visually identical to the great rhombidodecacron. It has 60 intersecting cross quadrilateral faces, 120 edges, and 62 vertices. Its faces are darts. Part of each dart lies inside the solid, hence is invisible in solid models.
In geometry, the great triakis icosahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great stellated truncated dodecahedron. Its faces are isosceles triangles. Part of each triangle lies within the solid, hence is invisible in solid models.
In geometry, the great pentakis dodecahedron is a nonconvex isohedral polyhedron.
In geometry, the medial disdyakis triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform truncated dodecadodecahedron. It has 120 triangular faces.
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |
