| Neotoma albigula varia | |
|---|---|
Scientific classification  | |
| Kingdom: | Animalia |
| Phylum: | Chordata |
| Class: | Mammalia |
| Order: | Rodentia |
| Family: | Cricetidae |
| Subfamily: | Neotominae |
| Genus: | Neotoma |
| Species: | |
| Subspecies: | N. a. varia |
| Trinomial name | |
| Neotoma albigula varia Burt, 1932 | |
The Turner Island woodrat (Neotoma albigula varia) is a subspecies of rodent in the family Cricetidae. It is found only in Mexico.
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after early 19th century mathematician Niels Henrik Abel.
The blue whale is a marine mammal belonging to the baleen whale suborder Mysticeti. Reaching a maximum confirmed length of 29.9 meters and weight of 173 tonnes, it is the largest animal known to have ever existed. The blue whale’s long and slender body can be various shades of grayish-blue dorsally and somewhat lighter underneath.
In mathematics, convolution is a mathematical operation on two functions that produces a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reversed and shifted. And the integral is evaluated for all values of shift, producing the convolution function.
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field whose value at a point is the vector whose components are the partial derivatives of at . That is, for , its gradient is defined at the point in n-dimensional space as the vector:
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest.
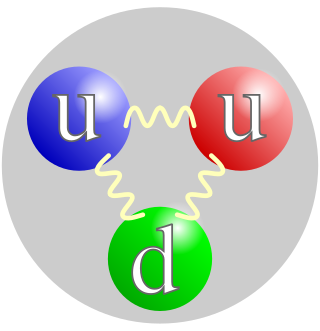
A proton is a subatomic particle, symbol
p
or
p+
, with a positive electric charge of +1e elementary charge and a mass slightly less than that of a neutron. Protons and neutrons, each with masses of approximately one atomic mass unit, are collectively referred to as "nucleons".
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
In physics, escape velocity is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a massive body, that is, to eventually reach an infinite distance from it. Escape velocity rises with the body's mass and falls with the escaping object's distance from its center. The escape velocity thus depends on how far the object has already traveled, and its calculation at a given distance takes into account the fact that without new acceleration it will slow down as it travels—due to the massive body's gravity—but it will never quite slow to a stop.
In mathematics, a Fourier series is a periodic function composed of harmonically related sinusoids, combined by a weighted summation. With appropriate weights, one cycle of the summation can be made to approximate an arbitrary function in that interval. As such, the summation is a synthesis of another function. The discrete-time Fourier transform is an example of Fourier series. The process of deriving weights that describe a given function is a form of Fourier analysis. For functions on unbounded intervals, the analysis and synthesis analogies are Fourier transform and inverse transform.
In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, it is often represented as the product of force and displacement. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.
Some Buddhist terms and concepts lack direct translations into English that cover the breadth of the original term. Below are given a number of important Buddhist terms, short definitions, and the languages in which they appear. In this list, an attempt has been made to organize terms by their original form and give translations and synonyms in other languages along with the definition.
In the mathematical field of differential geometry, one definition of a metric tensor is a type of function which takes as input a pair of tangent vectors v and w at a point of a surface and produces a real number scalar g(v, w) in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean space. In the same way as a dot product, metric tensors are used to define the length of and angle between tangent vectors. Through integration, the metric tensor allows one to define and compute the length of curves on the manifold.
This gallery of sovereign state flags shows the national or state flags of sovereign states that appear on the list of sovereign states. For other flags, please see flags of active autonomist and secessionist movements, flags of extinct states and gallery of flags of dependent territories. Each flag is depicted as if the flagpole is positioned on the left of the flag, except for those of Iran, Iraq and Saudi Arabia which are depicted with the hoist to the right.
The density of air or atmospheric density, denoted ρ, is the mass per unit volume of Earth's atmosphere. Air density, like air pressure, decreases with increasing altitude. It also changes with variation in atmospheric pressure, temperature and humidity. At 101.325 kPa (abs) and 15°C, air has a density of approximately 1.225 kg/m3, about 1/1000th that of water according to ISA.
In orbital mechanics, mean motion is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass. While nominally a mean, and theoretically so in the case of two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above conditions as calculated from the current gravitational and geometric circumstances of the body's constantly-changing, perturbed orbit.
 | This Neotoma article is a stub. You can help Wikipedia by expanding it. |