
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.
In mathematics, the uniformization theorem states that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generalization of the Riemann mapping theorem from simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.
In differential geometry, a quaternion-Kähler manifold (or quaternionic Kähler manifold) is a Riemannian 4n-manifold whose Riemannian holonomy group is a subgroup of Sp(n)·Sp(1) for some . Here Sp(n) is the sub-group of consisting of those orthogonal transformations that arise by left-multiplication by some quaternionic matrix, while the group of unit-length quaternions instead acts on quaternionic -space by right scalar multiplication. The Lie group generated by combining these actions is then abstractly isomorphic to .
In mathematics, a (real) Monge–Ampère equation is a nonlinear second-order partial differential equation of special kind. A second-order equation for the unknown function u of two variables x,y is of Monge–Ampère type if it is linear in the determinant of the Hessian matrix of u and in the second-order partial derivatives of u. The independent variables (x,y) vary over a given domain D of R2. The term also applies to analogous equations with n independent variables. The most complete results so far have been obtained when the equation is elliptic.
In the mathematical fields of differential geometry and geometric analysis, inverse mean curvature flow (IMCF) is a geometric flow of submanifolds of a Riemannian or pseudo-Riemannian manifold. It has been used to prove a certain case of the Riemannian Penrose inequality, which is of interest in general relativity.
Discrete differential geometry is the study of discrete counterparts of notions in differential geometry. Instead of smooth curves and surfaces, there are polygons, meshes, and simplicial complexes. It is used in the study of computer graphics, geometry processing and topological combinatorics.

In differential geometry, a triply periodic minimal surface (TPMS) is a minimal surface in that is invariant under a rank-3 lattice of translations.
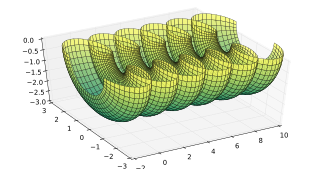
In differential geometry, constant-mean-curvature (CMC) surfaces are surfaces with constant mean curvature. This includes minimal surfaces as a subset, but typically they are treated as special case.

Gerhard Huisken is a German mathematician whose research concerns differential geometry and partial differential equations. He is known for foundational contributions to the theory of the mean curvature flow, including Huisken's monotonicity formula, which is named after him. With Tom Ilmanen, he proved a version of the Riemannian Penrose inequality, which is a special case of the more general Penrose conjecture in general relativity.
Henry Christian Wente was an American mathematician, known for his 1986 discovery of the Wente torus, an immersed constant-mean-curvature surface whose existence disproved a conjecture of Heinz Hopf.

Jürgen Jost is a German mathematician specializing in geometry. He has been a director of the Max Planck Institute for Mathematics in the Sciences in Leipzig since 1996.

Manfredo Perdigão do Carmo was a Brazilian mathematician. He spent most of his career at IMPA and is seen as the doyen of differential geometry in Brazil.
Ravindra Shripad Kulkarni is an Indian mathematician, specializing in differential geometry. He is known for the Kulkarni–Nomizu product.
Anthony Joseph Tromba is an American mathematician, specializing in partial differential equations, differential geometry, and the calculus of variations.

William Hamilton Meeks III is an American mathematician, specializing in differential geometry and minimal surfaces.
David Allen Hoffman is an American mathematician whose research concerns differential geometry. He is an adjunct professor at Stanford University. In 1985, together with William Meeks, he proved that Costa's surface was embedded. He is a fellow of the American Mathematical Society since 2018, for "contributions to differential geometry, particularly minimal surface theory, and for pioneering the use of computer graphics as an aid to research." He was awarded the Chauvenet Prize in 1990 for his expository article "The Computer-Aided Discovery of New Embedded Minimal Surfaces". He obtained his Ph.D. from Stanford University in 1971 under the supervision of Robert Osserman.
In the mathematical fields of differential geometry and geometric analysis, the Gauss curvature flow is a geometric flow for oriented hypersurfaces of Riemannian manifolds. In the case of curves in a two-dimensional manifold, it is identical with the curve shortening flow. The mean curvature flow is a different geometric flow which also has the curve shortening flow as a special case.
Katrin Leschke is a German mathematician specialising in differential geometry and known for her work on quaternionic analysis and Willmore surfaces. She works in England as a reader in mathematics at the University of Leicester, where she also heads the "Maths Meets Arts Tiger Team", an interdisciplinary group for the popularisation of mathematics, and led the "m:iv" project of international collaboration on minimal surfaces.








