In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, the Boolean satisfiability problem (SAT), satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research focusing on the resolution of particular forms of the constraint satisfaction problem.
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time.
In computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete. That is, it is in NP, and any problem in NP can be reduced in polynomial time by a deterministic Turing machine to the Boolean satisfiability problem.
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable or not. Horn-satisfiability and Horn clauses are named after Alfred Horn.
In computational complexity theory, Karp's 21 NP-complete problems are a set of computational problems which are NP-complete. In his 1972 paper, "Reducibility Among Combinatorial Problems", Richard Karp used Stephen Cook's 1971 theorem that the boolean satisfiability problem is NP-complete to show that there is a polynomial time many-one reduction from the boolean satisfiability problem to each of 21 combinatorial and graph theoretical computational problems, thereby showing that they are all NP-complete. This was one of the first demonstrations that many natural computational problems occurring throughout computer science are computationally intractable, and it drove interest in the study of NP-completeness and the P versus NP problem.
In logic and computer science, the Davis–Putnam algorithm was developed by Martin Davis and Hilary Putnam for checking the validity of a first-order logic formula using a resolution-based decision procedure for propositional logic. Since the set of valid first-order formulas is recursively enumerable but not recursive, there exists no general algorithm to solve this problem. Therefore, the Davis–Putnam algorithm only terminates on valid formulas. Today, the term "Davis–Putnam algorithm" is often used synonymously with the resolution-based propositional decision procedure that is actually only one of the steps of the original algorithm.
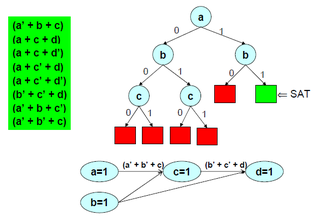
In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.
In computer science, GSAT and WalkSAT are local search algorithms to solve Boolean satisfiability problems.
The Karloff–Zwick algorithm, in computational complexity theory, is a randomised approximation algorithm taking an instance of MAX-3SAT Boolean satisfiability problem as input. If the instance is satisfiable, then the expected weight of the assignment found is at least 7/8 of optimal. There is strong evidence that the algorithm achieves 7/8 of optimal even on unsatisfiable MAX-3SAT instances. Howard Karloff and Uri Zwick presented the algorithm in 1997.
In computational complexity theory, the maximum satisfiability problem (MAX-SAT) is the problem of determining the maximum number of clauses, of a given Boolean formula in conjunctive normal form, that can be made true by an assignment of truth values to the variables of the formula. It is a generalization of the Boolean satisfiability problem, which asks whether there exists a truth assignment that makes all clauses true.

In constraint satisfaction, local search is an incomplete method for finding a solution to a problem. It is based on iteratively improving an assignment of the variables until all constraints are satisfied. In particular, local search algorithms typically modify the value of a variable in an assignment at each step. The new assignment is close to the previous one in the space of assignment, hence the name local search.
In computer science and formal methods, a SAT solver is a computer program which aims to solve the Boolean satisfiability problem. On input a formula over Boolean variables, such as "(x or y) and (x or not y)", a SAT solver outputs whether the formula is satisfiable, meaning that there are possible values of x and y which make the formula true, or unsatisfiable, meaning that there are no such values of x and y. In this case, the formula is satisfiable when x is true, so the solver should return "satisfiable". Since the introduction of algorithms for SAT in the 1960s, modern SAT solvers have grown into complex software artifacts involving a large number of heuristics and program optimizations to work efficiently.
MAXEkSAT is a problem in computational complexity theory that is a maximization version of the Boolean satisfiability problem 3SAT. In MAXEkSAT, each clause has exactly k literals, each with distinct variables, and is in conjunctive normal form. These are called k-CNF formulas. The problem is to determine the maximum number of clauses that can be satisfied by a truth assignment to the variables in the clauses.
In computer science, the Sharp Satisfiability Problem is the problem of counting the number of interpretations that satisfy a given Boolean formula, introduced by Valiant in 1979. In other words, it asks in how many ways the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. For example, the formula is satisfiable by three distinct boolean value assignments of the variables, namely, for any of the assignments, , and, we have
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption that was formulated by Impagliazzo & Paturi (1999). It states that satisfiability of 3-CNF Boolean formulas cannot be solved in subexponential time, . More precisely, the usual form of the hypothesis asserts the existence of a number such that all algorithms that correctly solve this problem require time at least The exponential time hypothesis, if true, would imply that P ≠ NP, but it is a stronger statement. It implies that many computational problems are equivalent in complexity, in the sense that if one of them has a subexponential time algorithm then they all do, and that many known algorithms for these problems have optimal or near-optimal time complexity.
In theoretical computer science, the circuit satisfiability problem is the decision problem of determining whether a given Boolean circuit has an assignment of its inputs that makes the output true. In other words, it asks whether the inputs to a given Boolean circuit can be consistently set to 1 or 0 such that the circuit outputs 1. If that is the case, the circuit is called satisfiable. Otherwise, the circuit is called unsatisfiable. In the figure to the right, the left circuit can be satisfied by setting both inputs to be 1, but the right circuit is unsatisfiable.
Stefan Szeider is an Austrian computer scientist who works on the areas of algorithms, computational complexity, theoretical computer science, and more specifically on propositional satisfiability, constraint satisfaction problems, and parameterised complexity. He is a full professor at the Faculty of Informatics at the Vienna University of Technology, the head of the Algorithms and Complexity Group, and co-chair of the Vienna Center for Logic and Algorithms (VCLA) of TU Wien.

In computer science, the planar 3-satisfiability problem (abbreviated PLANAR 3SAT or PL3SAT) is an extension of the classical Boolean 3-satisfiability problem to a planar incidence graph. In other words, it asks whether the variables of a given Boolean formula—whose incidence graph consisting of variables and clauses can be embedded on a plane—can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.



