Related Research Articles
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, Boolean satisfiability problem (SAT), the satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research focusing on the resolution of particular forms of the constraint satisfaction problem.

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time.
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable or not. Horn-satisfiability and Horn clauses are named after Alfred Horn.
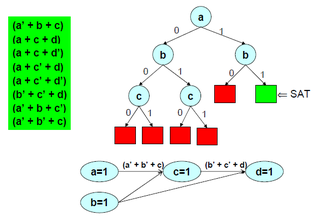
In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.
In computational complexity theory, the PCP theorem states that every decision problem in the NP complexity class has probabilistically checkable proofs of constant query complexity and logarithmic randomness complexity.
The Karloff–Zwick algorithm, in computational complexity theory, is a randomised approximation algorithm taking an instance of MAX-3SAT Boolean satisfiability problem as input. If the instance is satisfiable, then the expected weight of the assignment found is at least 7/8 of optimal. There is strong evidence that the algorithm achieves 7/8 of optimal even on unsatisfiable MAX-3SAT instances. Howard Karloff and Uri Zwick presented the algorithm in 1997.
In computational complexity, problems that are in the complexity class NP but are neither in the class P nor NP-complete are called NP-intermediate, and the class of such problems is called NPI. Ladner's theorem, shown in 1975 by Richard E. Ladner, is a result asserting that, if P ≠ NP, then NPI is not empty; that is, NP contains problems that are neither in P nor NP-complete. Since it is also true that if NPI problems exist, then P ≠ NP, it follows that P = NP if and only if NPI is empty.
In mathematical logic, given an unsatisfiable Boolean propositional formula in conjunctive normal form, a subset of clauses whose conjunction is still unsatisfiable is called an unsatisfiable core of the original formula.
In computer science and formal methods, a SAT solver is a computer program which aims to solve the Boolean satisfiability problem. On input a formula over Boolean variables, such as "(x or y) and ", a SAT solver outputs whether the formula is satisfiable, meaning that there are possible values of x and y which make the formula true, or unsatisfiable, meaning that there are no such values of x and y. In this case, the formula is satisfiable when x is true, so the solver should return "satisfiable". Since the introduction of algorithms for SAT in the 1960s, modern SAT solvers have grown into complex software artifacts involving a large number of heuristics and program optimizations to work efficiently.

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be bounded even for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
- Creation of a new vertex v with label i
- Disjoint union of two labeled graphs G and H
- Joining by an edge every vertex labeled i to every vertex labeled j, where i ≠ j
- Renaming label i to label j
In mathematical logic, a formula is satisfiable if it is true under some assignment of values to its variables. For example, the formula is satisfiable because it is true when and , while the formula is not satisfiable over the integers. The dual concept to satisfiability is validity; a formula is valid if every assignment of values to its variables makes the formula true. For example, is valid over the integers, but is not.
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption that was formulated by Impagliazzo & Paturi (1999). It states that satisfiability of 3-CNF Boolean formulas cannot be solved more quickly than exponential time in the worst case. The exponential time hypothesis, if true, would imply that P ≠ NP, but it is a stronger statement. It implies that many computational problems are equivalent in complexity, in the sense that if one of them has a subexponential time algorithm then they all do, and that many known algorithms for these problems have optimal or near-optimal time complexity.

Toniann Pitassi is a Canadian and American mathematician and computer scientist specializing in computational complexity theory. She is currently Jeffrey L. and Brenda Bleustein Professor of Engineering at Columbia University and was Bell Research Chair at the University of Toronto.
Derek Gordon Corneil is a Canadian mathematician and computer scientist, a professor emeritus of computer science at the University of Toronto, and an expert in graph algorithms and graph theory.
In the study of graph algorithms, Courcelle's theorem is the statement that every graph property definable in the monadic second-order logic of graphs can be decided in linear time on graphs of bounded treewidth. The result was first proved by Bruno Courcelle in 1990 and independently rediscovered by Borie, Parker & Tovey (1992). It is considered the archetype of algorithmic meta-theorems.
Uwe Schöning is a retired German computer scientist, known for his research in computational complexity theory.
Helmut Veith was an Austrian computer scientist who worked on the areas of computer-aided verification, software engineering, computer security, and logic in computer science. He was a Professor of Informatics at the Vienna University of Technology, Austria.
Agata Ciabattoni is an Italian mathematical logician specializing in non-classical logic. She is a full professor at the Institute of Logic and Computation of the Faculty of Informatics at the Vienna University of Technology, and a co-chair of the Vienna Center for Logic and Algorithms of TU Wien (VCLA).
References
- 1 2 "Faculty of Informatics, TU Wien" . Retrieved 13 January 2017.
- ↑ "Stefan Szeider - Algorithms and Complexity Group" . Retrieved 9 January 2017.
- ↑ "Computerwissenschafter der TU Wien wollen internationale Marke werden". Der Standard (in German). 25 January 2012. Retrieved 20 April 2020.
- ↑ "Stefan Szeider - The Mathematics Genealogy Project". Mathematics Genealogy Project . Retrieved 9 January 2017.
- 1 2 3 "Stefan Szeider". LogiCS. Retrieved 9 January 2017.
- ↑ "What does "insoluble" mean here? Prof. Stefan Szeider in portrait" . Retrieved 13 January 2017.
- ↑ "Algorithmen bestimmen unser Leben". Futurezone.at (in German). February 8, 2012. Retrieved 9 January 2017.
- ↑ "Zentrum für Grundlagen der Informatik". Der Standard (in German). 31 January 2012. Retrieved 9 January 2017.
- ↑ "Stefan Szeider - Professor, Head of Algorithms and Complexity Group, TU Wien". Google Scholar . Retrieved 9 January 2017.
- ↑ "Stefan Szeider - Computer Science Bibliography". DBLP .
- ↑ Gaspers, Serge; Szeider, Stefan (2012). "The Multivariate Algorithmic Revolution and Beyond". Backdoors to Satisfaction. pp. 287–317. CiteSeerX 10.1.1.747.5422 . doi:10.1007/978-3-642-30891-8_15. ISBN 978-3-642-30890-1. S2CID 6905561.
- ↑ Gaspers, Serge (22 April 2016). "Backdoors to SAT". Encyclopedia of Algorithms. Springer New York. pp. 167–170. doi:10.1007/978-1-4939-2864-4_781. ISBN 978-1-4939-2863-7.
- ↑ Samer, Marko; Szeider, Stefan (18 December 2008). "Backdoor Sets of Quantified Boolean Formulas". Journal of Automated Reasoning . 42 (1): 77–97. CiteSeerX 10.1.1.452.5953 . doi:10.1007/s10817-008-9114-5. S2CID 13030704.
- ↑ Fellows, Michael R.; Rosamond, Frances A.; Rotics, Udi; Szeider, Stefan (January 2009). "Clique-Width is NP-Complete". SIAM Journal on Discrete Mathematics . 23 (2): 909–939. doi:10.1137/070687256.
- ↑ Szeider, Stefan (December 2004). "Minimal unsatisfiable formulas with bounded clause-variable difference are fixed-parameter tractable" (PDF). Journal of Computer and System Sciences . 69 (4): 656–674. doi:10.1016/j.jcss.2004.04.009.
- ↑ Fleischner, Herbert; Kullmann, Oliver; Szeider, Stefan (October 2002). "Polynomial-time recognition of minimal unsatisfiable formulas with fixed clause-variable difference". Theoretical Computer Science . 289 (1): 503–516. doi: 10.1016/S0304-3975(01)00337-1 .