Clique-width

Last updated January 29, 2023

In graph theory, the clique-width of a graph $G$ is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be bounded even for dense graphs. It is defined as the minimum number of labels needed to construct $G$ by means of the following 4 operations :

Creation of a new vertex $v$ with label $i$ (denoted by $i (v)$ )
Disjoint union of two labeled graphs $G$ and $H$ (denoted by $G\oplus H$ )
Joining by an edge every vertex labeled $i$ to every vertex labeled $j$ (denoted by $η (i, j)$ ), where $i \neq j$
Renaming label $i$ to label $j$ (denoted by $ρ (i, j)$ )

Graphs of bounded clique-width include the cographs and distance-hereditary graphs. Although it is NP-hard to compute the clique-width when it is unbounded, and unknown whether it can be computed in polynomial time when it is bounded, efficient approximation algorithms for clique-width are known. Based on these algorithms and on Courcelle's theorem, many graph optimization problems that are NP-hard for arbitrary graphs can be solved or approximated quickly on the graphs of bounded clique-width.

The construction sequences underlying the concept of clique-width were formulated by Courcelle, Engelfriet, and Rozenberg in 1990^[1] and by Wanke (1994). The name "clique-width" was used for a different concept by Chlebíková (1992). By 1993, the term already had its present meaning.^[2]

Special classes of graphs

Cographs are exactly the graphs with clique-width at most 2.^[3] Every distance-hereditary graph has clique-width at most 3. However, the clique-width of unit interval graphs is unbounded (based on their grid structure).^[4] Similarly, the clique-width of bipartite permutation graphs is unbounded (based on similar grid structure).^[5] Based on the characterization of cographs as the graphs with no induced subgraph isomorphic to a path with four vertices, the clique-width of many graph classes defined by forbidden induced subgraphs has been classified.^[6]

Other graphs with bounded clique-width include the $k$ -leaf powers for bounded values of $k$ ; these are the induced subgraphs of the leaves of a tree $T$ in the graph power $T k$ . However, leaf powers with unbounded exponents do not have bounded clique-width.^[7]

Bounds

Courcelle & Olariu (2000) and Corneil & Rotics (2005) proved the following bounds on the clique-width of certain graphs:

If a graph has clique-width at most $k$ , then so does every induced subgraph of the graph.^[8]
The complement graph of a graph of clique-width $k$ has clique-width at most $2 k$ .^[9]
The graphs of treewidth $w$ have clique-width at most $3 \cdot 2 w - 1$ . The exponential dependence in this bound is necessary: there exist graphs whose clique-width is exponentially larger than their treewidth.^[10] In the other direction, graphs of bounded clique-width can have unbounded treewidth; for instance, $n$ -vertex complete graphs have clique-width 2 but treewidth $n - 1$ . However, graphs of clique-width $k$ that have no complete bipartite graph $K t, t$ as a subgraph have treewidth at most $3 k (t - 1) - 1$ . Therefore, for every family of sparse graphs, having bounded treewidth is equivalent to having bounded clique-width.^[11]
Another graph parameter, the rank-width, is bounded in both directions by the clique-width: rank-width ≤ clique-width ≤ 2^{rank-width + 1}.^[12]

Additionally, if a graph $G$ has clique-width $k$ , then the graph power $G c$ has clique-width at most $2 kc k$ .^[13] Although there is an exponential gap in both the bound for clique-width from treewidth and the bound for clique-width of graph powers, these bounds do not compound each other: if a graph $G$ has treewidth $w$ , then $G c$ has clique-width at most $2(c + 1) w + 1 - 2$ , only singly exponential in the treewidth.^[14]

Computational complexity

Unsolved problem in mathematics:

Can graphs of bounded clique-width be recognized in polynomial time?

(more unsolved problems in mathematics)

Many optimization problems that are NP-hard for more general classes of graphs may be solved efficiently by dynamic programming on graphs of bounded clique-width, when a construction sequence for these graphs is known.^[15]^[16] In particular, every graph property that can be expressed in MSO₁ monadic second-order logic (a form of logic allowing quantification over sets of vertices) has a linear-time algorithm for graphs of bounded clique-width, by a form of Courcelle's theorem.^[16]

It is also possible to find optimal graph colorings or Hamiltonian cycles for graphs of bounded clique-width in polynomial time, when a construction sequence is known, but the exponent of the polynomial increases with the clique-width, and evidence from computational complexity theory shows that this dependence is likely to be necessary.^[17] The graphs of bounded clique-width are $χ$ -bounded, meaning that their chromatic number is at most a function of the size of their largest clique.^[18]

The graphs of clique-width three can be recognized, and a construction sequence found for them, in polynomial time using an algorithm based on split decomposition.^[19] For graphs of unbounded clique-width, it is NP-hard to compute the clique-width exactly, and also NP-hard to obtain an approximation with sublinear additive error.^[20] However, when the clique-width is bounded, it is possible to obtain a construction sequence of bounded width (exponentially larger than the actual clique-width) in polynomial time,^[21] in particular in quadratic time in the number of vertices.^[22] It remains open whether the exact clique-width, or a tighter approximation to it, can be calculated in fixed-parameter tractable time, whether it can be calculated in polynomial time for every fixed bound on the clique-width, or even whether the graphs of clique-width four can be recognized in polynomial time.^[20]

Related width parameters

The theory of graphs of bounded clique-width resembles that for graphs of bounded treewidth, but unlike treewidth allows for dense graphs. If a family of graphs has bounded clique-width, then either it has bounded treewidth or every complete bipartite graph is a subgraph of a graph in the family.^[11] Treewidth and clique-width are also connected through the theory of line graphs: a family of graphs has bounded treewidth if and only if their line graphs have bounded clique-width.^[23]

The graphs of bounded clique-width also have bounded twin-width.^[24]

Notes

↑ Courcelle, Engelfriet & Rozenberg (1993).
↑ Courcelle (1993).
↑ Courcelle & Olariu (2000).
↑ Golumbic & Rotics (2000).
↑ Brandstädt & Lozin (2003).
↑ Brandstädt et al. (2005); Brandstädt et al. (2006).
↑ Brandstädt & Hundt (2008); Gurski & Wanke (2009).
↑ Courcelle & Olariu (2000), Corollary 3.3.
↑ Courcelle & Olariu (2000), Theorem 4.1.
↑ Corneil & Rotics (2005), strengthening Courcelle & Olariu (2000), Theorem 5.5.
1 2 Gurski & Wanke (2000).
↑ Oum & Seymour (2006).
↑ Todinca (2003).
↑ Gurski & Wanke (2009).
↑ Cogis & Thierry (2005).
1 2 Courcelle, Makowsky & Rotics (2000).
↑ Fomin et al. (2010).
↑ Dvořák & Král' (2012).
↑ Corneil et al. (2012).
1 2 Fellows et al. (2009).
↑ Oum & Seymour (2006); Hliněný & Oum (2008); Oum (2008); Fomin & Korhonen (2022).
↑ Fomin & Korhonen (2022).
↑ Gurski & Wanke (2007).
↑ Bonnet et al. (2022).

Related Research Articles

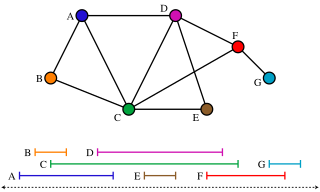
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

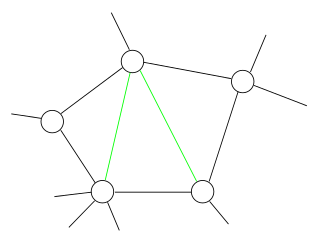
<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

In graph theory, the Hadwiger number of an undirected graph $G$ is the size of the largest complete graph that can be obtained by contracting edges of $G$ . Equivalently, the Hadwiger number $h (G)$ is the largest number $n$ for which the complete graph $K n$ is a minor of $G$ , a smaller graph obtained from $G$ by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of $G$ or the homomorphism degree of $G$ . It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of $G$ .

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly $k$ are called $k$ -trees, and the graphs with treewidth at most $k$ are called partial $k$ -trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph $G$ is, informally, a representation of $G$ as a "thickened" path graph, and the pathwidth of $G$ is a number that measures how much the path was thickened to form $G$ . More formally, a path-decomposition is a sequence of subsets of vertices of $G$ such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

<span class="mw-page-title-main">Branch-decomposition</span> Hierarchical clustering of graph edges

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

In graph theory, a clique cover or partition into cliques of a given undirected graph is a partition of the vertices into cliques, subsets of vertices within which every two vertices are adjacent. A minimum clique cover is a clique cover that uses as few cliques as possible. The minimum $k$ for which a clique cover exists is called the clique cover number of the given graph.

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.

In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.

In the mathematical fields of graph theory and combinatorics, a matching polynomial is a generating function of the numbers of matchings of various sizes in a graph. It is one of several graph polynomials studied in algebraic graph theory.

Derek Gordon Corneil is a Canadian mathematician and computer scientist, a professor emeritus of computer science at the University of Toronto, and an expert in graph algorithms and graph theory.

In the study of graph algorithms, Courcelle's theorem is the statement that every graph property definable in the monadic second-order logic of graphs can be decided in linear time on graphs of bounded treewidth. The result was first proved by Bruno Courcelle in 1990 and independently rediscovered by Borie, Parker & Tovey (1992). It is considered the archetype of algorithmic meta-theorems.

In graph theory, a bramble for an undirected graph $G$ is a family of connected subgraphs of $G$ that all touch each other: for every pair of disjoint subgraphs, there must exist an edge in $G$ that has one endpoint in each subgraph. The order of a bramble is the smallest size of a hitting set, a set of vertices of $G$ that has a nonempty intersection with each of the subgraphs. Brambles may be used to characterize the treewidth of $G$ .

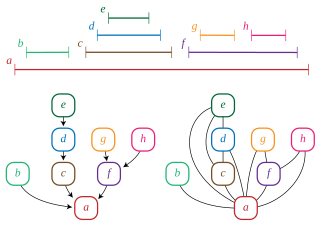
In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

In the mathematical fields of graph theory and finite model theory, the logic of graphs deals with formal specifications of graph properties using sentences of mathematical logic. There are several variations in the types of logical operation that can be used in these sentences. The first-order logic of graphs concerns sentences in which the variables and predicates concern individual vertices and edges of a graph, while monadic second-order graph logic allows quantification over sets of vertices or edges. Logics based on least fixed point operators allow more general predicates over tuples of vertices, but these predicates can only be constructed through fixed-point operators, restricting their power.

In the mathematical area of graph theory, a $k$ -leaf power of a tree $T$ is a graph $G$ whose vertices are the leaves of $T$ and whose edges connect pairs of leaves whose distance in $T$ is at most $k$ . That is, $G$ is an induced subgraph of the graph power $, induced by the leaves of T . For a graph G constructed in this way, T is called a k -leaf root of G .$

The twin-width of an undirected graph is a natural number associated with the graph, used to study the parameterized complexity of graph algorithms. Intuitively, it measures how similar the graph is to a cograph, a type of graph that can be reduced to a single vertex by repeatedly merging together twins, vertices that have the same neighbors. The twin-width is defined from a sequence of repeated mergers where the vertices are not required to be twins, but have nearly equal sets of neighbors.

References

Bonnet, Édouard; Kim, Eun Jung; Thomassé, Stéphan; Watrigant, Rémi (2022), "Twin-width I: Tractable FO model checking", Journal of the ACM , 69 (1): A3:1–A3:46, arXiv: 2004.14789 , doi:10.1145/3486655, MR 4402362
Brandstädt, A.; Dragan, F.F.; Le, H.-O.; Mosca, R. (2005), "New graph classes of bounded clique-width", Theory of Computing Systems, 38 (5): 623–645, CiteSeerX 10.1.1.3.5994 , doi:10.1007/s00224-004-1154-6, S2CID 2309695 .
Brandstädt, A.; Engelfriet, J.; Le, H.-O.; Lozin, V.V. (2006), "Clique-width for 4-vertex forbidden subgraphs", Theory of Computing Systems, 39 (4): 561–590, doi:10.1007/s00224-005-1199-1, S2CID 20050455 .
Brandstädt, Andreas; Hundt, Christian (2008), "Ptolemaic graphs and interval graphs are leaf powers", LATIN 2008: Theoretical informatics, Lecture Notes in Comput. Sci., vol. 4957, Springer, Berlin, pp. 479–491, doi:10.1007/978-3-540-78773-0_42, MR 2472761 .
Brandstädt, A.; Lozin, V.V. (2003), "On the linear structure and clique-width of bipartite permutation graphs", Ars Combinatoria , 67: 273–281, CiteSeerX 10.1.1.16.2000 .
Chlebíková, J. (1992), "On the tree-width of a graph", Acta Mathematica Universitatis Comenianae, New Series, 61 (2): 225–236, CiteSeerX 10.1.1.30.3900 , MR 1205875 .
Cogis, O.; Thierry, E. (2005), "Computing maximum stable sets for distance-hereditary graphs", Discrete Optimization, 2 (2): 185–188, doi: 10.1016/j.disopt.2005.03.004 , MR 2155518 .
Corneil, Derek G.; Habib, Michel; Lanlignel, Jean-Marc; Reed, Bruce; Rotics, Udi (2012), "Polynomial-time recognition of clique-width $\leq 3$ graphs", Discrete Applied Mathematics , 160 (6): 834–865, doi: 10.1016/j.dam.2011.03.020 , MR 2901093 .
Corneil, Derek G.; Rotics, Udi (2005), "On the relationship between clique-width and treewidth", SIAM Journal on Computing , 34 (4): 825–847, doi:10.1137/S0097539701385351, MR 2148860 .
Courcelle, Bruno; Engelfriet, Joost; Rozenberg, Grzegorz (1993), "Handle-rewriting hypergraph grammars", Journal of Computer and System Sciences, 46 (2): 218–270, doi: 10.1016/0022-0000(93)90004-G , MR 1217156 . Presented in preliminary form in Graph grammars and their application to computer science (Bremen, 1990), MR 1431281.
Courcelle, B. (1993), "Monadic second-order logic and hypergraph orientation", Proceedings of Eighth Annual IEEE Symposium on Logic in Computer Science (LICS '93), pp. 179–190, doi:10.1109/LICS.1993.287589, S2CID 39254668 .
Courcelle, B.; Makowsky, J. A.; Rotics, U. (2000), "Linear time solvable optimization problems on graphs on bounded clique width", Theory of Computing Systems, 33 (2): 125–150, CiteSeerX 10.1.1.414.1845 , doi:10.1007/s002249910009, S2CID 15402031 .
Courcelle, B.; Olariu, S. (2000), "Upper bounds to the clique width of graphs", Discrete Applied Mathematics , 101 (1–3): 77–144, doi: 10.1016/S0166-218X(99)00184-5 .
Dvořák, Zdeněk; Král', Daniel (2012), "Classes of graphs with small rank decompositions are χ-bounded", Electronic Journal of Combinatorics, 33 (4): 679–683, arXiv: 1107.2161 , doi:10.1016/j.ejc.2011.12.005, S2CID 5530520
Fellows, Michael R.; Rosamond, Frances A.; Rotics, Udi; Szeider, Stefan (2009), "Clique-width is NP-complete", SIAM Journal on Discrete Mathematics , 23 (2): 909–939, doi:10.1137/070687256, MR 2519936 .
Fomin, Fedor V.; Golovach, Petr A.; Lokshtanov, Daniel; Saurabh, Saket (2010), "Intractability of clique-width parameterizations", SIAM Journal on Computing , 39 (5): 1941–1956, CiteSeerX 10.1.1.220.1712 , doi:10.1137/080742270, MR 2592039 .
Fomin, Fedor V.; Korhonen, Tuukka (2022), "Fast FPT-approximation of branchwidth", Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, ACM, pp. 886–899, arXiv: 2111.03492 , doi:10.1145/3519935.3519996 .
Golumbic, Martin Charles; Rotics, Udi (2000), "On the clique-width of some perfect graph classes", International Journal of Foundations of Computer Science, 11 (3): 423–443, doi:10.1142/S0129054100000260, MR 1792124 .
Gurski, Frank; Wanke, Egon (2000), "The tree-width of clique-width bounded graphs without $K n,n$ ", in Brandes, Ulrik; Wagner, Dorothea (eds.), Graph-Theoretic Concepts in Computer Science: 26th International Workshop, WG 2000, Konstanz, Germany, June 15–17, 2000, Proceedings, Lecture Notes in Computer Science, vol. 1928, Berlin: Springer, pp. 196–205, doi:10.1007/3-540-40064-8_19, MR 1850348 .
Gurski, Frank; Wanke, Egon (2007), "Line graphs of bounded clique-width", Discrete Mathematics , 307 (22): 2734–2754, doi: 10.1016/j.disc.2007.01.020 .
Gurski, Frank; Wanke, Egon (2009), "The NLC-width and clique-width for powers of graphs of bounded tree-width", Discrete Applied Mathematics , 157 (4): 583–595, doi: 10.1016/j.dam.2008.08.031 , MR 2499471 .
Hliněný, Petr; Oum, Sang-il (2008), "Finding branch-decompositions and rank-decompositions", SIAM Journal on Computing , 38 (3): 1012–1032, CiteSeerX 10.1.1.94.2272 , doi:10.1137/070685920, MR 2421076 .
Oum, Sang-il; Seymour, Paul (2006), "Approximating clique-width and branch-width", Journal of Combinatorial Theory , Series B, 96 (4): 514–528, doi: 10.1016/j.jctb.2005.10.006 , MR 2232389 .
Oum, Sang-il (2008), "Approximating rank-width and clique-width quickly", ACM Transactions on Algorithms , 5 (1): Art. 10, 20, CiteSeerX 10.1.1.574.8156 , doi:10.1145/1435375.1435385, MR 2479181 .
Todinca, Ioan (2003), "Coloring powers of graphs of bounded clique-width", Graph-theoretic concepts in computer science, Lecture Notes in Comput. Sci., vol. 2880, Springer, Berlin, pp. 370–382, doi:10.1007/978-3-540-39890-5_32, MR 2080095 .
Wanke, Egon (1994), " $k$ -NLC graphs and polynomial algorithms", Discrete Applied Mathematics , 54 (2–3): 251–266, doi: 10.1016/0166-218X(94)90026-4 , MR 1300250 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FOOTNOTECourcelleEngelfrietRozenberg1993-1] Courcelle, Engelfriet & Rozenberg (1993).

[FOOTNOTECourcelle1993-2] Courcelle (1993).

[FOOTNOTECourcelleOlariu2000-3] Courcelle & Olariu (2000).

[FOOTNOTEGolumbicRotics2000-4] Golumbic & Rotics (2000).

[FOOTNOTEBrandstädtLozin2003-5] Brandstädt & Lozin (2003).

[6] Brandstädt et al. (2005); Brandstädt et al. (2006).

[7] Brandstädt & Hundt (2008); Gurski & Wanke (2009).

[8] Courcelle & Olariu (2000), Corollary 3.3.

[9] Courcelle & Olariu (2000), Theorem 4.1.

[10] Corneil & Rotics (2005), strengthening Courcelle & Olariu (2000), Theorem 5.5.

[FOOTNOTEGurskiWanke2000-11] 1 2 Gurski & Wanke (2000).

[FOOTNOTEOumSeymour2006-12] Oum & Seymour (2006).

[FOOTNOTETodinca2003-13] Todinca (2003).

[FOOTNOTEGurskiWanke2009-14] Gurski & Wanke (2009).

[FOOTNOTECogisThierry2005-15] Cogis & Thierry (2005).

[FOOTNOTECourcelleMakowskyRotics2000-16] 1 2 Courcelle, Makowsky & Rotics (2000).

[FOOTNOTEFominGolovachLokshtanovSaurabh2010-17] Fomin et al. (2010).

[FOOTNOTEDvořákKrál'2012-18] Dvořák & Král' (2012).

[FOOTNOTECorneilHabibLanlignelReed2012-19] Corneil et al. (2012).

[FOOTNOTEFellowsRosamondRoticsSzeider2009-20] 1 2 Fellows et al. (2009).

[21] Oum & Seymour (2006); Hliněný & Oum (2008); Oum (2008); Fomin & Korhonen (2022).

[FOOTNOTEFominKorhonen2022-22] Fomin & Korhonen (2022).

[FOOTNOTEGurskiWanke2007-23] Gurski & Wanke (2007).

[FOOTNOTEBonnetKimThomasséWatrigant2022-24] Bonnet et al. (2022).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]