Leaf power

Last updated August 27, 2023

In the mathematical area of graph theory, a $k$ -leaf power of a tree $T$ is a graph $G$ whose vertices are the leaves of $T$ and whose edges connect pairs of leaves whose distance in $T$ is at most $k$ . That is, $G$ is an induced subgraph of the graph power $T^{k}$ , induced by the leaves of $T$ . For a graph $G$ constructed in this way, $T$ is called a $k$ -leaf root of $G$ .

Related classes of graphs

Since powers of strongly chordal graphs are strongly chordal and trees are strongly chordal, it follows that leaf powers are strongly chordal graphs.^[2] Actually, leaf powers form a proper subclass of strongly chordal graphs; a graph is a leaf power if and only if it is a fixed tolerance NeST graph^[3] and such graphs are a proper subclass of strongly chordal graphs.^[4]

In Brandstädt et al. (2010) it is shown that interval graphs and the larger class of rooted directed path graphs are leaf powers. The indifference graphs are exactly the leaf powers whose underlying trees are caterpillar trees.

The $k$ -leaf powers for bounded values of $k$ have bounded clique-width, but this is not true of leaf powers with unbounded exponents.^[5]

Structure and recognition

A graph is a 3-leaf power if and only if it is a (bull, dart, gem)-free chordal graph.^[6] Based on this characterization and similar ones, 3-leaf powers can be recognized in linear time.^[7]

Characterizations of 4-leaf powers are given by Rautenbach (2006) and Brandstädt, Le & Sritharan (2008), which also enable linear time recognition. Recognition of the 5-leaf and 6-leaf power graphs are also solved in linear time by Chang and Ko (2007)^[8] and Ducoffe (2018),^[9] respectively.

For $k \geq 7$ the recognition problem of $k$ -leaf powers was unsolved for a long time, but Lafond (2021) showed that $k$ -leaf powers can be recognized in polynomial time for any fixed $k$ . However, the high dependency on the parameter $k$ makes this algorithm unsuitable for practical use.

Also, it has been proved that recognizing $k$ -leaf powers is fixed-parameter tractable when parameterized by $k$ and the degeneracy of the input graph.^[10]

Notes

↑ Nishimura, Ragde & Thilikos (2002).
↑ Dahlhaus & Duchet (1987); Lubiw (1987); Raychaudhuri (1992).
↑ Brandstädt et al. (2010); Hayward, Kearney & Malton (2002).
↑ Broin & Lowe (1986); Bibelnieks & Dearing (1993).
↑ Brandstädt & Hundt (2008); Gurski & Wanke (2009).
↑ Dom et al. (2006); Rautenbach (2006)
↑ Brandstädt & Le (2006).
↑ Ko, Ming-Tat; Chang, Maw-Shang (2007-06-21). "The 3-Steiner Root Problem". Graph-Theoretic Concepts in Computer Science. Lecture Notes in Computer Science. Vol. 4769. Springer, Berlin, Heidelberg. pp. 109–120. doi:10.1007/978-3-540-74839-7_11. ISBN 9783540748380.
↑ Ducoffe, Guillaume (2018-10-04). "Polynomial-time Recognition of 4-Steiner Powers". arXiv: 1810.02304 [cs.CC].
↑ Eppstein, David; Havvaei, Elham (2020-08-01). "Parameterized Leaf Power Recognition via Embedding into Graph Products". Algorithmica. 82 (8): 2337–2359. doi:10.1007/s00453-020-00720-8. ISSN 1432-0541. S2CID 218988055.

Related Research Articles

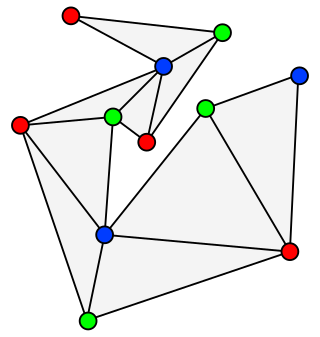
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

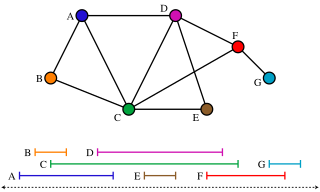
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

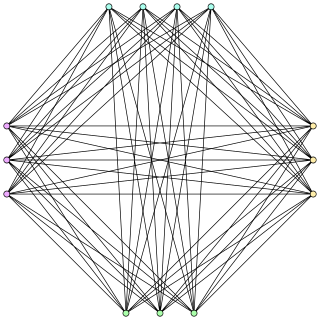
In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

In graph theory, the metric dimension of a graph G is the minimum cardinality of a subset S of vertices such that all other vertices are uniquely determined by their distances to the vertices in S. Finding the metric dimension of a graph is an NP-hard problem; the decision version, determining whether the metric dimension is less than a given value, is NP-complete.

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly $k$ are called $k$ -trees, and the graphs with treewidth at most $k$ are called partial $k$ -trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, the Grundy number or Grundy chromatic number of an undirected graph is the maximum number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first available color, using a vertex ordering chosen to use as many colors as possible. Grundy numbers are named after P. M. Grundy, who studied an analogous concept for directed graphs in 1939. The undirected version was introduced by Christen & Selkow (1979).

In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order. Comparability graphs have also been called transitively orientable graphs, partially orderable graphs, containment graphs, and divisor graphs. An incomparability graph is an undirected graph that connects pairs of elements that are not comparable to each other in a partial order.

In graph theory, the strong product is a way of combining two graphs to make a larger graph. Two vertices are adjacent in the strong product when they come from pairs of vertices in the factor graphs that are either adjacent or identical. The strong product is one of several different graph product operations that have been studied in graph theory. The strong product of any two graphs can be constructed as the union of two other products of the same two graphs, the Cartesian product of graphs and the tensor product of graphs.

In graph theory, the clique-width of a graph $G$ is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct $G$ by means of the following 4 operations :

Creation of a new vertex $v$ with label $i$ (denoted by $i (v)$ )
Disjoint union of two labeled graphs $G$ and $H$ (denoted by $)$
Joining by an edge every vertex labeled $i$ to every vertex labeled $j$ (denoted by $η (i, j)$ ), where $i \neq j$
Renaming label $i$ to label $j$ (denoted by $ρ (i, j)$ )

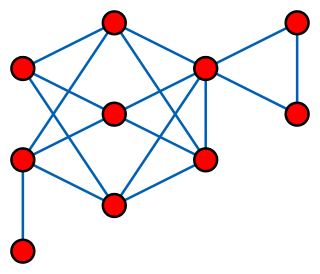
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

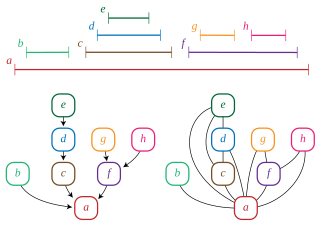
In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.

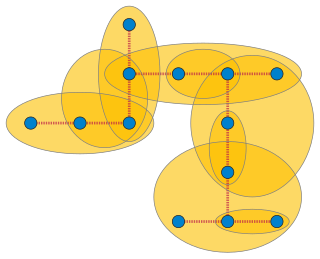
<span class="mw-page-title-main">Hypertree</span> Generalization of tree graphs to hypergraphs

In the mathematical field of graph theory, a hypergraph $H$ is called a hypertree if it admits a host graph $T$ such that $T$ is a tree. In other words, $H$ is a hypertree if there exists a tree $T$ such that every hyperedge of $H$ is the set of vertices of a connected subtree of $T$ . Hypertrees have also been called arboreal hypergraphs or tree hypergraphs.

In the mathematical area of graph theory, an undirected graph $G$ is strongly chordal if it is a chordal graph and every cycle of even length in $G$ has an odd chord, i.e., an edge that connects two vertices that are an odd distance (>1) apart from each other in the cycle.

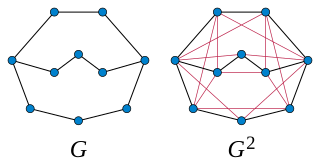
In graph theory, a branch of mathematics, the $k$ th power $G k$ of an undirected graph $G$ is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in $G$ is at most $k$ . Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: $G 2$ is called the square of $G$ , $G 3$ is called the cube of $G$ , etc.

In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

In the mathematical area of graph theory, a chordal bipartite graph is a bipartite graph B = (X,Y,E) in which every cycle of length at least 6 in B has a chord, i.e., an edge that connects two vertices that are a distance > 1 apart from each other in the cycle. A better name would be weakly chordal and bipartite since chordal bipartite graphs are in general not chordal as the induced cycle of length 4 shows.

Andreas Brandstädt is a German mathematician and computer scientist.

In the mathematical area of graph theory, an undirected graph $G$ is dually chordal if the hypergraph of its maximal cliques is a hypertree. The name comes from the fact that a graph is chordal if and only if the hypergraph of its maximal cliques is the dual of a hypertree. Originally, these graphs were defined by maximum neighborhood orderings and have a variety of different characterizations. Unlike for chordal graphs, the property of being dually chordal is not hereditary, i.e., induced subgraphs of a dually chordal graph are not necessarily dually chordal, and a dually chordal graph is in general not a perfect graph.

In graph theory, a split of an undirected graph is a cut whose cut-set forms a complete bipartite graph. A graph is prime if it has no splits. The splits of a graph can be collected into a tree-like structure called the split decomposition or join decomposition, which can be constructed in linear time. This decomposition has been used for fast recognition of circle graphs and distance-hereditary graphs, as well as for other problems in graph algorithms.

In graph theory, an induced matching or strong matching is a subset of the edges of an undirected graph that do not share any vertices and includes every edge connecting any two vertices in the subset.

References

Bibelnieks, E.; Dearing, P.M. (1993), "Neighborhood subtree tolerance graphs", Discrete Applied Mathematics, 43: 13–26, doi:10.1016/0166-218X(93)90165-K .
Brandstädt, Andreas; Hundt, Christian (2008), "Ptolemaic graphs and interval graphs are leaf powers", LATIN 2008: Theoretical informatics, Lecture Notes in Comput. Sci., vol. 4957, Springer, Berlin, pp. 479–491, doi:10.1007/978-3-540-78773-0_42, ISBN 978-3-540-78772-3, MR 2472761 .
Brandstädt, Andreas; Hundt, Christian; Mancini, Federico; Wagner, Peter (2010), "Rooted directed path graphs are leaf powers", Discrete Mathematics , 310 (4): 897–910, doi: 10.1016/j.disc.2009.10.006 .
Brandstädt, Andreas; Le, Van Bang (2006), "Structure and linear time recognition of 3-leaf powers", Information Processing Letters , 98 (4): 133–138, CiteSeerX 10.1.1.144.3486 , doi:10.1016/j.ipl.2006.01.004 .
Brandstädt, Andreas; Le, Van Bang; Sritharan, R. (2008), "Structure and linear time recognition of 4-leaf powers", ACM Transactions on Algorithms , 5: 1–22, doi:10.1145/1435375.1435386, S2CID 6114466 .
Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy (1999), Graph Classes: A Survey , SIAM Monographs on Discrete Mathematics and Applications, ISBN 978-0-89871-432-6 .
Broin, M.W.; Lowe, T.J. (1986), "Neighborhood subtree tolerance graphs", SIAM J. Algebr. Discrete Methods, 7: 348–357, doi:10.1137/0607039 .
Dahlhaus, E.; Duchet, P. (1987), "On strongly chordal graphs", Ars Combinatoria , 24 B: 23–30.
Dahlhaus, E.; Manuel, P. D.; Miller, M. (1998), "A characterization of strongly chordal graphs", Discrete Mathematics , 187 (1–3): 269–271, doi:10.1016/S0012-365X(97)00268-9 .
Dom, M.; Guo, J.; Hüffner, F.; Niedermeier, R. (2006), "Error compensation in leaf root problems", Algorithmica , 44 (4): 363–381, CiteSeerX 10.1.1.218.490 , doi:10.1007/s00453-005-1180-z, S2CID 75279 .
Farber, M. (1983), "Characterizations of strongly chordal graphs", Discrete Mathematics , 43 (2–3): 173–189, doi:10.1016/0012-365X(83)90154-1 .
Gurski, Frank; Wanke, Egon (2009), "The NLC-width and clique-width for powers of graphs of bounded tree-width", Discrete Applied Mathematics , 157 (4): 583–595, doi: 10.1016/j.dam.2008.08.031 , MR 2499471 .
Hayward, R.B.; Kearney, P.E.; Malton, A. (2002), "NeST graphs", Discrete Applied Mathematics, 121 (1–3): 139–153, doi: 10.1016/s0166-218x(01)00207-4 .
Lafond, Manuel (2021), "Recognizing k-leaf powers in polynomial time, for constant k", Proceedings of the 2022 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA) : 1384–1410, arXiv: 2110.15421 .
Lubiw, A. (1987), "Doubly lexical orderings of matrices", SIAM Journal on Computing , 16 (5): 854–879, doi:10.1137/0216057 .
McKee, T. A. (1999), "A new characterization of strongly chordal graphs", Discrete Mathematics , 205 (1–3): 245–247, doi: 10.1016/S0012-365X(99)00107-7 .
Nishimura, N.; Ragde, P.; Thilikos, D.M. (2002), "On graph powers for leaf-labeled trees", Journal of Algorithms , 42: 69–108, CiteSeerX 10.1.1.43.1127 , doi:10.1006/jagm.2001.1195 .
Rautenbach, D. (2006), "Some remarks about leaf roots", Discrete Mathematics , 306 (13): 1456–1461, doi:10.1016/j.disc.2006.03.030 .
Raychaudhuri, A. (1992), "On powers of strongly chordal graphs and circular arc graphs", Ars Combinatoria, 34: 147–160.
Eppstein, D.; Havvaei, H. (2020), "Parameterized Leaf Power Recognition via Embedding into Graph Products", Algorithmica , 82 (8): 2337–2359, doi:10.1007/s00453-020-00720-8, S2CID 218988055 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FOOTNOTENishimuraRagdeThilikos2002-1] Nishimura, Ragde & Thilikos (2002).

[2] Dahlhaus & Duchet (1987); Lubiw (1987); Raychaudhuri (1992).

[3] Brandstädt et al. (2010); Hayward, Kearney & Malton (2002).

[4] Broin & Lowe (1986); Bibelnieks & Dearing (1993).

[5] Brandstädt & Hundt (2008); Gurski & Wanke (2009).

[6] Dom et al. (2006); Rautenbach (2006)

[FOOTNOTEBrandstädtLe2006-7] Brandstädt & Le (2006).

[8] Ko, Ming-Tat; Chang, Maw-Shang (2007-06-21). "The 3-Steiner Root Problem". Graph-Theoretic Concepts in Computer Science. Lecture Notes in Computer Science. Vol. 4769. Springer, Berlin, Heidelberg. pp. 109–120. doi:10.1007/978-3-540-74839-7_11. ISBN 9783540748380.

[9] Ducoffe, Guillaume (2018-10-04). "Polynomial-time Recognition of 4-Steiner Powers". arXiv: 1810.02304 [cs.CC].

[10] Eppstein, David; Havvaei, Elham (2020-08-01). "Parameterized Leaf Power Recognition via Embedding into Graph Products". Algorithmica. 82 (8): 2337–2359. doi:10.1007/s00453-020-00720-8. ISSN 1432-0541. S2CID 218988055.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]