Indifference graph

Last updated November 08, 2023

In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other.^[1] Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals (intervals none of which contains any other one). Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

Equivalent characterizations

The finite indifference graphs may be equivalently characterized as

The intersection graphs of unit intervals,^[1]
The intersection graphs of sets of intervals no two of which are nested (one containing the other),^[1]^[2]
The claw-free interval graphs,^[1]^[2]
The graphs that do not have an induced subgraph isomorphic to a claw K_1,3, net (a triangle with a degree-one vertex adjacent to each of the triangle vertices), sun (a triangle surrounded by three other triangles that each share one edge with the central triangle), or hole (cycle of length four or more),^[3]
The incomparability graphs of semiorders,^[1]
The undirected graphs that have a linear order such that, for every three vertices ordered $u$ – $v$ – $w$ , if $uw$ is an edge then so are $uv$ and $vw$ ^[4]
The graphs with no astral triple, three vertices connected pairwise by paths that avoid the third vertex and also do not contain two consecutive neighbors of the third vertex,^[5]
The graphs in which each connected component contains a path in which each maximal clique of the component forms a contiguous sub-path,^[6]
The graphs whose vertices can be numbered in such a way that every shortest path forms a monotonic sequence,^[6]
The graphs whose adjacency matrices can be ordered such that, in each row and each column, the nonzeros of the matrix form a contiguous interval adjacent to the main diagonal of the matrix.^[7]
The induced subgraphs of powers of chordless paths.^[8]
The leaf powers having a leaf root which is a caterpillar.^[8]

For infinite graphs, some of these definitions may differ.

Properties

Because they are special cases of interval graphs, indifference graphs have all the properties of interval graphs; in particular they are a special case of the chordal graphs and of the perfect graphs. They are also a special case of the circle graphs, something that is not true of interval graphs more generally.

In the Erdős–Rényi model of random graphs, an $n$ -vertex graph whose number of edges is significantly less than $n^{2/3}$ will be an indifference graph with high probability, whereas a graph whose number of edges is significantly more than $n^{2/3}$ will not be an indifference graph with high probability.^[9]

The bandwidth of an arbitrary graph $G$ is one less than the size of the maximum clique in an indifference graph that contains $G$ as a subgraph and is chosen to minimize the size of the maximum clique.^[10] This property parallels similar relations between pathwidth and interval graphs, and between treewidth and chordal graphs. A weaker notion of width, the clique-width, may be arbitrarily large on indifference graphs.^[11] However, every proper subclass of the indifference graphs that is closed under induced subgraphs has bounded clique-width.^[12]

Every connected indifference graph has a Hamiltonian path.^[13] An indifference graph has a Hamiltonian cycle if and only if it is biconnected.^[14]

Indifference graphs obey the reconstruction conjecture: they are uniquely determined by their vertex-deleted subgraphs.^[15]

Algorithms

As with higher dimensional unit disk graphs, it is possible to transform a set of points into their indifference graph, or a set of unit intervals into their unit interval graph, in linear time as measured in terms of the size of the output graph. The algorithm rounds the points (or interval centers) down to the nearest smaller integer, uses a hash table to find all pairs of points whose rounded integers are within one of each other (the fixed-radius near neighbors problem), and filters the resulting list of pairs for the ones whose unrounded values are also within one of each other.^[16]

It is possible to test whether a given graph is an indifference graph in linear time, by using PQ trees to construct an interval representation of the graph and then testing whether a vertex ordering derived from this representation satisfies the properties of an indifference graph.^[4] It is also possible to base a recognition algorithm for indifference graphs on chordal graph recognition algorithms.^[14] Several alternative linear time recognition algorithms are based on breadth-first search or lexicographic breadth-first search rather than on the relation between indifference graphs and interval graphs.^[17]^[18]^[19]^[20]

Once the vertices have been sorted by the numerical values that describe an indifference graph (or by the sequence of unit intervals in an interval representation) the same ordering can be used to find an optimal graph coloring for these graphs, to solve the shortest path problem, and to construct Hamiltonian paths and maximum matchings, all in linear time.^[4] A Hamiltonian cycle can be found from a proper interval representation of the graph in time $O(n\log n)$ ,^[13] but when the graph itself is given as input, the same problem admits linear-time solution that can be generalized to interval graphs.^[21]^[22]

List coloring remains NP-complete even when restricted to indifference graphs.^[23] However, it is fixed-parameter tractable when parameterized by the total number of colors in the input.^[12]

Applications

In mathematical psychology, indifference graphs arise from utility functions, by scaling the function so that one unit represents a difference in utilities small enough that individuals can be assumed to be indifferent to it. In this application, pairs of items whose utilities have a large difference may be partially ordered by the relative order of their utilities, giving a semiorder.^[1]^[24]

In bioinformatics, the problem of augmenting a colored graph to a properly colored unit interval graph can be used to model the detection of false negatives in DNA sequence assembly from complete digests.^[25]

Related Research Articles

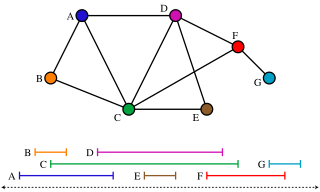
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In the mathematical discipline of graph theory, the line graph of an undirected graph $G$ is another graph $L(G)$ that represents the adjacencies between edges of $G$ . $L(G)$ is constructed in the following way: for each edge in $G$ , make a vertex in $L(G)$ ; for every two edges in $G$ that have a vertex in common, make an edge between their corresponding vertices in $L(G)$ .

<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In the mathematical field of graph theory, the complement or inverse of a graph $G$ is a graph $H$ on the same vertices such that two distinct vertices of $H$ are adjacent if and only if they are not adjacent in $G$ . That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.

In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

In graph theory, a circle graph is the intersection graph of a chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.

In geometric graph theory, a unit disk graph is the intersection graph of a family of unit disks in the Euclidean plane. That is, it is a graph with one vertex for each disk in the family, and with an edge between two vertices whenever the corresponding vertices lie within a unit distance of each other.

In graph theory, a path decomposition of a graph $G$ is, informally, a representation of $G$ as a "thickened" path graph, and the pathwidth of $G$ is a number that measures how much the path was thickened to form $G$ . More formally, a path-decomposition is a sequence of subsets of vertices of $G$ such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

<span class="mw-page-title-main">Intersection graph</span> Graph representing intersections between given sets

In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.

<span class="mw-page-title-main">Handshaking lemma</span> Every graph has evenly many odd vertices

In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees equals twice the number of edges in the graph. Both results were proven by Leonhard Euler (1736) in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.

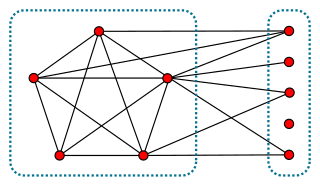
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földes and Hammer, and independently introduced by Tyshkevich and Chernyak (1979), where they called these graphs "polar graphs".

<span class="mw-page-title-main">Threshold graph</span> Graph formed by adding isolated or universal vertices

In graph theory, a threshold graph is a graph that can be constructed from a one-vertex graph by repeated applications of the following two operations:

Addition of a single isolated vertex to the graph.
Addition of a single dominating vertex to the graph, i.e. a single vertex that is connected to all other vertices.

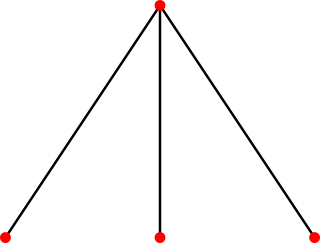
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

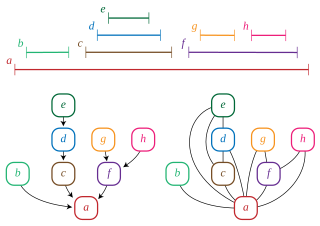
In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.

In the mathematical area of graph theory, an undirected graph $G$ is strongly chordal if it is a chordal graph and every cycle of even length in $G$ has an odd chord, i.e., an edge that connects two vertices that are an odd distance (>1) apart from each other in the cycle.

In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices are within distance 1 of a central path.

In the mathematical area of graph theory, a $k$ -leaf power of a tree $T$ is a graph $G$ whose vertices are the leaves of $T$ and whose edges connect pairs of leaves whose distance in $T$ is at most $k$ . That is, $G$ is an induced subgraph of the graph power $, induced by the leaves of T . For a graph G constructed in this way, T is called a k -leaf root of G .$

References

1 2 3 4 5 6 Roberts, Fred S. (1969), "Indifference graphs", Proof Techniques in Graph Theory (Proc. Second Ann Arbor Graph Theory Conf., Ann Arbor, Mich., 1968), Academic Press, New York, pp. 139–146, MR 0252267 .
1 2 Bogart, Kenneth P.; West, Douglas B. (1999), "A short proof that "proper = unit"", Discrete Mathematics , 201 (1–3): 21–23, arXiv: math/9811036 , doi:10.1016/S0012-365X(98)00310-0, MR 1687858 .
↑ Wegner, G. (1967), Eigenschaften der Nerven homologisch-einfacher Familien im Rⁿ, Ph.D. thesis, Göttingen, Germany: Göttingen University. As cited by Hell & Huang (2004).
1 2 3 Looges, Peter J.; Olariu, Stephan (1993), "Optimal greedy algorithms for indifference graphs", Computers & Mathematics with Applications, 25 (7): 15–25, doi: 10.1016/0898-1221(93)90308-I , MR 1203643 .
↑ Jackowski, Zygmunt (1992), "A new characterization of proper interval graphs", Discrete Mathematics , 105 (1–3): 103–109, doi: 10.1016/0012-365X(92)90135-3 , MR 1180196 .
1 2 Gutierrez, M.; Oubiña, L. (1996), "Metric characterizations of proper interval graphs and tree-clique graphs", Journal of Graph Theory, 21 (2): 199–205, doi:10.1002/(SICI)1097-0118(199602)21:2<199::AID-JGT9>3.0.CO;2-M, MR 1368745 .
↑ Mertzios, George B. (2008), "A matrix characterization of interval and proper interval graphs", Applied Mathematics Letters, 21 (4): 332–337, doi:10.1016/j.aml.2007.04.001, MR 2406509 .
1 2 Brandstädt, Andreas; Hundt, Christian; Mancini, Federico; Wagner, Peter (2010), "Rooted directed path graphs are leaf powers", Discrete Mathematics, 310: 897–910, doi: 10.1016/j.disc.2009.10.006 .
↑ Cohen, Joel E. (1982), "The asymptotic probability that a random graph is a unit interval graph, indifference graph, or proper interval graph", Discrete Mathematics , 40 (1): 21–24, doi: 10.1016/0012-365X(82)90184-4 , MR 0676708 .
↑ Kaplan, Haim; Shamir, Ron (1996), "Pathwidth, bandwidth, and completion problems to proper interval graphs with small cliques", SIAM Journal on Computing, 25 (3): 540–561, doi:10.1137/S0097539793258143, MR 1390027 .
↑ Golumbic, Martin Charles; Rotics, Udi (1999), "The clique-width of unit interval graphs is unbounded", Proceedings of the Thirtieth Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Boca Raton, FL, 1999), Congressus Numerantium, vol. 140, pp. 5–17, MR 1745205 .
1 2 Lozin, Vadim V. (2008), "From tree-width to clique-width: excluding a unit interval graph", Algorithms and computation, Lecture Notes in Comput. Sci., vol. 5369, Springer, Berlin, pp. 871–882, doi:10.1007/978-3-540-92182-0_76, MR 2539978 .
1 2 Bertossi, Alan A. (1983), "Finding Hamiltonian circuits in proper interval graphs", Information Processing Letters, 17 (2): 97–101, doi:10.1016/0020-0190(83)90078-9, MR 0731128 .
1 2 Panda, B. S.; Das, Sajal K. (2003), "A linear time recognition algorithm for proper interval graphs", Information Processing Letters, 87 (3): 153–161, doi:10.1016/S0020-0190(03)00298-9, MR 1986780 .
↑ von Rimscha, Michael (1983), "Reconstructibility and perfect graphs", Discrete Mathematics, 47 (2–3): 283–291, doi: 10.1016/0012-365X(83)90099-7 , MR 0724667 .
↑ Bentley, Jon L.; Stanat, Donald F.; Williams, E. Hollins Jr. (1977), "The complexity of finding fixed-radius near neighbors", Information Processing Letters , 6 (6): 209–212, doi:10.1016/0020-0190(77)90070-9, MR 0489084 .
↑ Corneil, Derek G.; Kim, Hiryoung; Natarajan, Sridhar; Olariu, Stephan; Sprague, Alan P. (1995), "Simple linear time recognition of unit interval graphs", Information Processing Letters, 55 (2): 99–104, CiteSeerX 10.1.1.39.855 , doi:10.1016/0020-0190(95)00046-F, MR 1344787 .
↑ Herrera de Figueiredo, Celina M.; Meidanis, João; Picinin de Mello, Célia (1995), "A linear-time algorithm for proper interval graph recognition", Information Processing Letters, 56 (3): 179–184, doi:10.1016/0020-0190(95)00133-W, MR 1365411 .
↑ Corneil, Derek G. (2004), "A simple 3-sweep LBFS algorithm for the recognition of unit interval graphs", Discrete Applied Mathematics, 138 (3): 371–379, doi: 10.1016/j.dam.2003.07.001 , MR 2049655 .
↑ Hell, Pavol; Huang, Jing (2004), "Certifying LexBFS recognition algorithms for proper interval graphs and proper interval bigraphs", SIAM Journal on Discrete Mathematics , 18 (3): 554–570, doi:10.1137/S0895480103430259, MR 2134416 .
↑ Keil, J. Mark (1985), "Finding Hamiltonian circuits in interval graphs", Information Processing Letters, 20 (4): 201–206, doi:10.1016/0020-0190(85)90050-X, MR 0801816 .
↑ Ibarra, Louis (2009), "A simple algorithm to find Hamiltonian cycles in proper interval graphs", Information Processing Letters, 109 (18): 1105–1108, doi:10.1016/j.ipl.2009.07.010, MR 2552898 .
↑ Marx, Dániel (2006), "Precoloring extension on unit interval graphs", Discrete Applied Mathematics, 154 (6): 995–1002, doi: 10.1016/j.dam.2005.10.008 , MR 2212549 .
↑ Roberts, Fred S. (1970), "On nontransitive indifference", Journal of Mathematical Psychology, 7: 243–258, doi:10.1016/0022-2496(70)90047-7, MR 0258486 .
↑ Goldberg, Paul W.; Golumbic, Martin C.; Kaplan, Haim; Shamir, Ron (2009), "Four strikes against physical mapping of DNA", Journal of Computational Biology, 2 (2), doi:10.1089/cmb.1995.2.139, PMID 7497116 .

External links

Information System on Graph Class Inclusions: unit interval graph

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[roberts-1] 1 2 3 4 5 6 Roberts, Fred S. (1969), "Indifference graphs", Proof Techniques in Graph Theory (Proc. Second Ann Arbor Graph Theory Conf., Ann Arbor, Mich., 1968), Academic Press, New York, pp. 139–146, MR 0252267 .

[bogart-west-2] 1 2 Bogart, Kenneth P.; West, Douglas B. (1999), "A short proof that "proper = unit"", Discrete Mathematics , 201 (1–3): 21–23, arXiv: math/9811036 , doi:10.1016/S0012-365X(98)00310-0, MR 1687858 .

[3] Wegner, G. (1967), Eigenschaften der Nerven homologisch-einfacher Familien im Rⁿ, Ph.D. thesis, Göttingen, Germany: Göttingen University. As cited by Hell & Huang (2004).

[greedy-4] 1 2 3 Looges, Peter J.; Olariu, Stephan (1993), "Optimal greedy algorithms for indifference graphs", Computers & Mathematics with Applications, 25 (7): 15–25, doi: 10.1016/0898-1221(93)90308-I , MR 1203643 .

[5] Jackowski, Zygmunt (1992), "A new characterization of proper interval graphs", Discrete Mathematics , 105 (1–3): 103–109, doi: 10.1016/0012-365X(92)90135-3 , MR 1180196 .

[metric-6] 1 2 Gutierrez, M.; Oubiña, L. (1996), "Metric characterizations of proper interval graphs and tree-clique graphs", Journal of Graph Theory, 21 (2): 199–205, doi:10.1002/(SICI)1097-0118(199602)21:2<199::AID-JGT9>3.0.CO;2-M, MR 1368745 .

[7] Mertzios, George B. (2008), "A matrix characterization of interval and proper interval graphs", Applied Mathematics Letters, 21 (4): 332–337, doi:10.1016/j.aml.2007.04.001, MR 2406509 .

[leafroot-8] 1 2 Brandstädt, Andreas; Hundt, Christian; Mancini, Federico; Wagner, Peter (2010), "Rooted directed path graphs are leaf powers", Discrete Mathematics, 310: 897–910, doi: 10.1016/j.disc.2009.10.006 .

[9] Cohen, Joel E. (1982), "The asymptotic probability that a random graph is a unit interval graph, indifference graph, or proper interval graph", Discrete Mathematics , 40 (1): 21–24, doi: 10.1016/0012-365X(82)90184-4 , MR 0676708 .

[10] Kaplan, Haim; Shamir, Ron (1996), "Pathwidth, bandwidth, and completion problems to proper interval graphs with small cliques", SIAM Journal on Computing, 25 (3): 540–561, doi:10.1137/S0097539793258143, MR 1390027 .

[11] Golumbic, Martin Charles; Rotics, Udi (1999), "The clique-width of unit interval graphs is unbounded", Proceedings of the Thirtieth Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Boca Raton, FL, 1999), Congressus Numerantium, vol. 140, pp. 5–17, MR 1745205 .

[lozin-12] 1 2 Lozin, Vadim V. (2008), "From tree-width to clique-width: excluding a unit interval graph", Algorithms and computation, Lecture Notes in Comput. Sci., vol. 5369, Springer, Berlin, pp. 871–882, doi:10.1007/978-3-540-92182-0_76, MR 2539978 .

[bertossi-13] 1 2 Bertossi, Alan A. (1983), "Finding Hamiltonian circuits in proper interval graphs", Information Processing Letters, 17 (2): 97–101, doi:10.1016/0020-0190(83)90078-9, MR 0731128 .

[pandas-14] 1 2 Panda, B. S.; Das, Sajal K. (2003), "A linear time recognition algorithm for proper interval graphs", Information Processing Letters, 87 (3): 153–161, doi:10.1016/S0020-0190(03)00298-9, MR 1986780 .

[15] von Rimscha, Michael (1983), "Reconstructibility and perfect graphs", Discrete Mathematics, 47 (2–3): 283–291, doi: 10.1016/0012-365X(83)90099-7 , MR 0724667 .

[16] Bentley, Jon L.; Stanat, Donald F.; Williams, E. Hollins Jr. (1977), "The complexity of finding fixed-radius near neighbors", Information Processing Letters , 6 (6): 209–212, doi:10.1016/0020-0190(77)90070-9, MR 0489084 .

[17] Corneil, Derek G.; Kim, Hiryoung; Natarajan, Sridhar; Olariu, Stephan; Sprague, Alan P. (1995), "Simple linear time recognition of unit interval graphs", Information Processing Letters, 55 (2): 99–104, CiteSeerX 10.1.1.39.855 , doi:10.1016/0020-0190(95)00046-F, MR 1344787 .

[18] Herrera de Figueiredo, Celina M.; Meidanis, João; Picinin de Mello, Célia (1995), "A linear-time algorithm for proper interval graph recognition", Information Processing Letters, 56 (3): 179–184, doi:10.1016/0020-0190(95)00133-W, MR 1365411 .

[19] Corneil, Derek G. (2004), "A simple 3-sweep LBFS algorithm for the recognition of unit interval graphs", Discrete Applied Mathematics, 138 (3): 371–379, doi: 10.1016/j.dam.2003.07.001 , MR 2049655 .

[20] Hell, Pavol; Huang, Jing (2004), "Certifying LexBFS recognition algorithms for proper interval graphs and proper interval bigraphs", SIAM Journal on Discrete Mathematics , 18 (3): 554–570, doi:10.1137/S0895480103430259, MR 2134416 .

[21] Keil, J. Mark (1985), "Finding Hamiltonian circuits in interval graphs", Information Processing Letters, 20 (4): 201–206, doi:10.1016/0020-0190(85)90050-X, MR 0801816 .

[22] Ibarra, Louis (2009), "A simple algorithm to find Hamiltonian cycles in proper interval graphs", Information Processing Letters, 109 (18): 1105–1108, doi:10.1016/j.ipl.2009.07.010, MR 2552898 .

[23] Marx, Dániel (2006), "Precoloring extension on unit interval graphs", Discrete Applied Mathematics, 154 (6): 995–1002, doi: 10.1016/j.dam.2005.10.008 , MR 2212549 .

[24] Roberts, Fred S. (1970), "On nontransitive indifference", Journal of Mathematical Psychology, 7: 243–258, doi:10.1016/0022-2496(70)90047-7, MR 0258486 .

[25] Goldberg, Paul W.; Golumbic, Martin C.; Kaplan, Haim; Shamir, Ron (2009), "Four strikes against physical mapping of DNA", Journal of Computational Biology, 2 (2), doi:10.1089/cmb.1995.2.139, PMID 7497116 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]