Derek Corneil

Last updated
Derek G. Corneil
NationalityCanadian
Education
Scientific career
Fields
Institutions University of Toronto
Thesis Graph Isomorphism (1968)
Doctoral advisor Calvin Gotlieb
Doctoral students

Derek Gordon Corneil is a Canadian mathematician and computer scientist, a professor emeritus of computer science at the University of Toronto, and an expert in graph algorithms and graph theory.

Contents

Life

When he was leaving high school, Corneil was told by his English teacher that doing a degree in mathematics and physics was a bad idea, and that the best he could hope for was to go to a technical college. His interest in computer science began when, as an undergraduate student at Queens College, he heard that a computer was purchased by the London Life insurance company in London, Ontario, where his father worked. As a freshman, he took a summer job operating the UNIVAC Mark II at the company. One of his main responsibilities was to operate a printer. An opportunity for a programming job with the company sponsoring his college scholarship appeared soon after. It was a chance that Corneil jumped at after being denied a similar position at London Life. There was an initial mix-up at his job as his overseer thought that he knew how to program the UNIVAC Mark II, and so he would easily transition to doing the same for the company's newly acquired IBM 1401 machine. However, Corneil did not have the assumed programming background. Thus, in the two-week window that Corneil had been given to learn how to grasp programming the IBM 1401, he learned how to write code from scratch by relying heavily on the instruction manual. This experience pushed him further on his way as did a number of projects he worked on in that position later on. [1]

Corneil went on to earn a bachelor's degree in mathematics and physics from Queen's University in 1964. Initially he had planned to do his graduate studies before becoming a high school teacher, but his acceptance into the brand new graduate program in computer science at the University of Toronto changed that. At the University of Toronto, Corneil earned a master's degree and then in 1968 a doctorate in computer science under the supervision of Calvin Gotlieb. [2] [3] (His post-doctoral supervisor was Jaap Seidel.) It was during this time that Corneil became interested in graph theory. He and Gotlieb eventually became good friends. After postdoctoral studies at the Eindhoven University of Technology, Corneil returned to Toronto as a faculty member in 1970. [2] Before his retirement in 2010, [4] Corneil held many positions at the University of Toronto, including Department Chair of the Computer Science department (July 1985 to June 1990), Director of Research Initiatives of the Faculty of Arts and Science (July 1991 to March 1998), and Acting Vice President of Research and International Relations (September to December 1993). During his time as a professor, he was also a visiting professor at universities such as the University of British Columbia, Simon Fraser University, the Université de Grenoble and the Université de Montpellier.

Work

Corneil did his research in algorithmic graph theory and graph theory in general. He has overseen 49 theses and published over 100 papers on his own or with co-authors. These papers include:

A proof that recognizing graphs of small treewidth is NP-complete, [5]
The discovery of the cotree representation for cographs and of fast recognition algorithms for cographs, [6] [7]
Generating algorithms for graph isomorphism. [8] [9]
Algorithmic and structural properties of complement reducible graphs. [10]
Properties of asteroidal triple-free graphs. [11]
An algorithm to solve the problem of determining whether a graph is a partial graph of a k-tree. [12]
Results addressing graph theoretic, algorithmic, and complexity issues with regard to tree spanners. [13]
An explanation of the relationship between tree width and clique-width. [14]
Determining the diameter of restricted graph families. [15]
Outlining the structure of trapezoid graphs. [16]

As a professor emeritus, Corneil still does research and is also an editor of several publications such as Ars Combinatoria and SIAM Monographs on Discrete Mathematics and Applications.

Awards

He was inducted as a Fields Institute Fellow in 2004. [17]

Related Research Articles

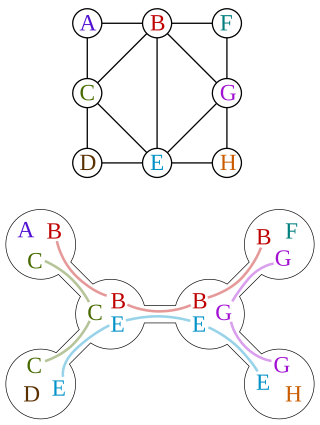
<span class="mw-page-title-main">Tree decomposition</span> Mapping of a graph into a tree

In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to define the treewidth of the graph and speed up solving certain computational problems on the graph.

<span class="mw-page-title-main">Outerplanar graph</span> Non-crossing graph with vertices on outer face

In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

<span class="mw-page-title-main">Complete coloring</span> Vertex coloring where every color pairing appears at least once

In graph theory, a complete coloring is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic numberψ(G) of a graph G is the maximum number of colors possible in any complete coloring of G.

<span class="mw-page-title-main">Chordal graph</span> Graph where all long cycles have a chord

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

<span class="mw-page-title-main">Cograph</span> Graph formed by complementation and disjoint union

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.

<span class="mw-page-title-main">Circle graph</span> Intersection graph of a chord diagram

In graph theory, a circle graph is the intersection graph of a chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.

In graph theory, the metric dimension of a graph G is the minimum cardinality of a subset S of vertices such that all other vertices are uniquely determined by their distances to the vertices in S. Finding the metric dimension of a graph is an NP-hard problem; the decision version, determining whether the metric dimension is less than a given value, is NP-complete.

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.

A tree k-spanner of a graph is a spanning subtree of in which the distance between every pair of vertices is at most times their distance in .

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

<span class="mw-page-title-main">Series–parallel graph</span> Recursively-formed graph with two terminal vertices

In graph theory, series–parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.

<span class="mw-page-title-main">Clique-width</span> Measure of graph complexity

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :

  1. Creation of a new vertex v with label i (denoted by i(v))
  2. Disjoint union of two labeled graphs G and H (denoted by )
  3. Joining by an edge every vertex labeled i to every vertex labeled j (denoted by η(i,j)), where i ≠ j
  4. Renaming label i to label j (denoted by ρ(i,j))
<span class="mw-page-title-main">Distance-hereditary graph</span> Graph whose induced subgraphs preserve distance

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

<span class="mw-page-title-main">Permutation graph</span> Graph representing a permutation

In the mathematical field of graph theory, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.

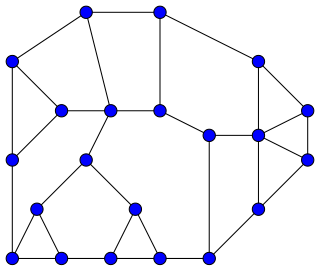
<span class="mw-page-title-main">Halin graph</span> Mathematical tree with cycle through leaves

In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

In computer science, lexicographic breadth-first search or Lex-BFS is a linear time algorithm for ordering the vertices of a graph. The algorithm is different from a breadth-first search, but it produces an ordering that is consistent with breadth-first search.

In graph theory, a branch of mathematics, a chordal completion of a given undirected graph G is a chordal graph, on the same vertex set, that has G as a subgraph. A minimal chordal completion is a chordal completion such that any graph formed by removing an edge would no longer be a chordal completion. A minimum chordal completion is a chordal completion with as few edges as possible.

Lorna Kay Stewart is a retired Canadian computer scientist and discrete mathematician whose research concerns algorithms in graph theory and special classes of graphs, including cographs, permutation graphs, interval graphs, comparability graphs and their complements, well-covered graphs, and asteroidal triple-free graphs. She earned her Ph.D. in 1985 at the University of Toronto under the supervision of Derek Corneil, and is a professor emerita at the University of Alberta.

References

  1. ↑ "Derek Corneil: Renowned and Esteemed Computer Science Professor Emeritus University of Toronto - Canadian IT Manager's Blog - Site Home - TechNet Blogs". Archived from the original on 2011-06-23. Retrieved 2012-02-19.
  2. 1 2 Biography, University of Toronto. Retrieved 1/8 February 2012.
  3. ↑ Derek Gordon Corneil at the Mathematics Genealogy Project
  4. ↑ "Derek Corneil: Retiring after 40 years with DCS" (PDF), @DCS, University of Toronto Department of Computer Science, 1 (3): 8, 2010.
  5. ↑ Arnborg, Stefan; Corneil, Derek G.; Proskurowski, Andrzej (1987), "Complexity of finding embeddings in a $k$-tree", SIAM Journal on Algebraic and Discrete Methods, 8 (2): 277–284, doi:10.1137/0608024, MR   0881187 .
  6. ↑ Corneil, D. G.; Lerchs, H.; Burlingham, L. Stewart (1981), "Complement reducible graphs", Discrete Applied Mathematics , 3 (3): 163–174, doi:10.1016/0166-218X(81)90013-5, MR   0619603
  7. ↑ Corneil, D. G.; Perl, Y.; Stewart, L. K. (1985), "A linear recognition algorithm for cographs", SIAM Journal on Computing, 14 (4): 926–934, doi:10.1137/0214065, MR   0807891 .
  8. ↑ Corneil, D. G.; Gotlieb, C. C. (1970), "An efficient algorithm for graph isomorphism", Journal of the ACM , 17: 51–64, CiteSeerX   10.1.1.453.3730 , doi:10.1145/321556.321562, MR   0278977, S2CID   207720001
  9. ↑ Read, Ronald C.; Corneil, Derek G. (1977), "The graph isomorphism disease", Journal of Graph Theory , 1 (4): 339–363, doi:10.1002/jgt.3190010410, MR   0485586 .
  10. ↑ Corneil, D.G.; Lerchs, H.; Burlingham, L.Stewart (1981). "Complement reducible graphs". Discrete Applied Mathematics. 3 (3): 163–174. doi:10.1016/0166-218X(81)90013-5.
  11. ↑ Corneil, Derek G.; Olariu, Stephan; Stewart, Lorna (1997). "Asteroidal Triple-Free Graphs". SIAM Journal on Discrete Mathematics. 10 (3): 399–430. doi:10.1137/S0895480193250125.
  12. ↑ Arnborg, Stefan; Corneil, Derek G.; Proskurowski, Andrzej (1987). "Complexity of Finding Embeddings in a k -Tree". SIAM Journal on Algebraic and Discrete Methods. 8 (2): 277–284. doi:10.1137/0608024.
  13. ↑ Cai, Leizhen; Corneil, Derek G. (1995). "Tree Spanners". SIAM Journal on Discrete Mathematics. 8 (3): 359–387. doi:10.1137/S0895480192237403.
  14. ↑ Corneil, Derek G.; Rotics, Udi (2005). "On the Relationship Between Clique-Width and Treewidth". SIAM Journal on Computing. 34 (4): 825–847. doi:10.1137/S0097539701385351.
  15. ↑ Corneil, Derek G.; Dragan, Feodor F.; Habib, Michel; Paul, Christophe (2001). "Diameter determination on restricted graph families" (PDF). Discrete Applied Mathematics. 113 (2–3): 143–166. doi:10.1016/S0166-218X(00)00281-X.
  16. ↑ Mertzios, George B.; Corneil, Derek G. (2011). "Vertex splitting and the recognition of trapezoid graphs" (PDF). Discrete Applied Mathematics. 159 (11): 1131–1147. doi:10.1016/j.dam.2011.03.023.
  17. ↑ Fields Institute Fellows. Retrieved 18 February 2012.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.