In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.
In geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.
In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
In geometry, lines in a plane or higher-dimensional space are concurrent if they intersect at a single point.
Thébault's theorem is the name given variously to one of the geometry problems proposed by the French mathematician Victor Thébault, individually known as Thébault's problem I, II, and III.
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson. The concept was first published, however, by William Wallace in 1799, and is sometimes called the Wallace line.
The Finsler–Hadwiger theorem is statement in Euclidean plane geometry that describes a third square derived from any two squares that share a vertex. The theorem is named after Paul Finsler and Hugo Hadwiger, who published it in 1937 as part of the same paper in which they published the Hadwiger–Finsler inequality relating the side lengths and area of a triangle.
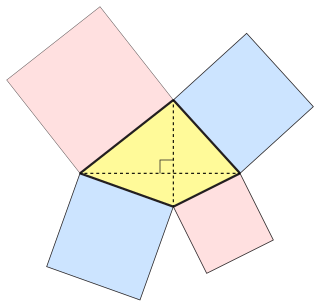
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.
In Euclidean geometry, an equidiagonal quadrilateral is a convex quadrilateral whose two diagonals have equal length. Equidiagonal quadrilaterals were important in ancient Indian mathematics, where quadrilaterals were classified first according to whether they were equidiagonal and then into more specialized types.
In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle. This is a circle that is tangent to each of the polygon's sides. The dual polygon of a tangential polygon is a cyclic polygon, which has a circumscribed circle passing through each of its vertices.
In geometry, the Petr–Douglas–Neumann theorem is a result concerning arbitrary planar polygons. The theorem asserts that a certain procedure when applied to an arbitrary polygon always yields a regular polygon having the same number of sides as the initial polygon. The theorem was first published by Karel Petr (1868–1950) of Prague in 1908. The theorem was independently rediscovered by Jesse Douglas (1897–1965) in 1940 and also by B H Neumann (1909–2002) in 1941. The naming of the theorem as Petr–Douglas–Neumann theorem, or as the PDN-theorem for short, is due to Stephen B Gray. This theorem has also been called Douglas's theorem, the Douglas–Neumann theorem, the Napoleon–Douglas–Neumann theorem and Petr's theorem.
Bottema's theorem is a theorem in plane geometry by the Dutch mathematician Oene Bottema.
