
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space . A vector field on a plane can be visualized as a collection of arrows with given magnitudes and directions, each attached to a point on the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout three dimensional space, such as the wind, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.

In geometry, a geodesic is a curve representing in some sense the shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line".

A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold is a manifold which assembles all the tangent vectors in . As a set, it is given by the disjoint union of the tangent spaces of . That is,

In Riemannian geometry, an exponential map is a map from a subset of a tangent space TpM of a Riemannian manifold M to M itself. The (pseudo) Riemannian metric determines a canonical affine connection, and the exponential map of the (pseudo) Riemannian manifold is given by the exponential map of this connection.
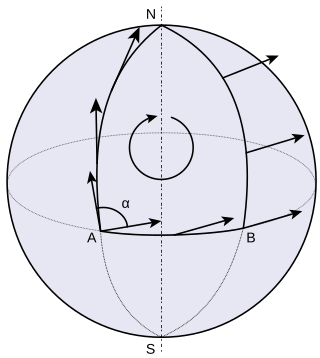
In differential geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection, then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the connection.
In differential geometry, the Lie derivative, named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a tensor field, along the flow defined by another vector field. This change is coordinate invariant and therefore the Lie derivative is defined on any differentiable manifold.
In mathematics, a symplectomorphism or symplectic map is an isomorphism in the category of symplectic manifolds. In classical mechanics, a symplectomorphism represents a transformation of phase space that is volume-preserving and preserves the symplectic structure of phase space, and is called a canonical transformation.
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the geometry of the base manifold using a solder form. Cartan connections describe the geometry of manifolds modelled on homogeneous spaces.
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.
Let be a smooth map between smooth manifolds and . Then there is an associated linear map from the space of 1-forms on to the space of 1-forms on . This linear map is known as the pullback, and is frequently denoted by . More generally, any covariant tensor field – in particular any differential form – on may be pulled back to using .
This is a glossary of terms specific to differential geometry and differential topology. The following three glossaries are closely related:

In differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. Connections are among the simplest methods of defining differentiation of the sections of vector bundles.
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a principal G-subbundle of the tangent frame bundle FM (or GL(M)) of M.
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations.

In differential geometry, pushforward is a linear approximation of smooth maps on tangent spaces. Suppose that is a smooth map between smooth manifolds; then the differential of at a point , denoted , is, in some sense, the best linear approximation of near . It can be viewed as a generalization of the total derivative of ordinary calculus. Explicitly, the differential is a linear map from the tangent space of at to the tangent space of at , . Hence it can be used to push tangent vectors on forward to tangent vectors on . The differential of a map is also called, by various authors, the derivative or total derivative of .

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
In mathematics, the vector flow refers to a set of closely related concepts of the flow determined by a vector field. These appear in a number of different contexts, including differential topology, Riemannian geometry and Lie group theory. These related concepts are explored in a spectrum of articles:
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fiber bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fiber bundle, but nevertheless, linear connections may be viewed as a special case. Another important special case of Ehresmann connections are principal connections on principal bundles, which are required to be equivariant in the principal Lie group action.
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle (TTM,πTTM,TM) of the total space TM of the tangent bundle (TM,πTM,M) of a smooth manifold M . A note on notation: in this article, we denote projection maps by their domains, e.g., πTTM : TTM → TM. Some authors index these maps by their ranges instead, so for them, that map would be written πTM.
In physics, general covariant transformations are symmetries of gravitation theory on a world manifold . They are gauge transformations whose parameter functions are vector fields on . From the physical viewpoint, general covariant transformations are treated as particular (holonomic) reference frame transformations in general relativity. In mathematics, general covariant transformations are defined as particular automorphisms of so-called natural fiber bundles.








