
AWK is a domain-specific language designed for text processing and typically used as a data extraction and reporting tool. Like sed and grep, it is a filter, and is a standard feature of most Unix-like operating systems.

A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.
A fuzzy control system is a control system based on fuzzy logic—a mathematical system that analyzes analog input values in terms of logical variables that take on continuous values between 0 and 1, in contrast to classical or digital logic, which operates on discrete values of either 1 or 0.
Controllability is an important property of a control system and plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control.
The Vienna Development Method (VDM) is one of the longest-established formal methods for the development of computer-based systems. Originating in work done at the IBM Laboratory Vienna in the 1970s, it has grown to include a group of techniques and tools based on a formal specification language—the VDM Specification Language (VDM-SL). It has an extended form, VDM++, which supports the modeling of object-oriented and concurrent systems. Support for VDM includes commercial and academic tools for analyzing models, including support for testing and proving properties of models and generating program code from validated VDM models. There is a history of industrial usage of VDM and its tools and a growing body of research in the formalism has led to notable contributions to the engineering of critical systems, compilers, concurrent systems and in logic for computer science.
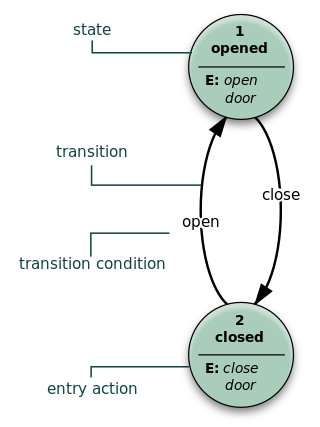
A state diagram is used in computer science and related fields to describe the behavior of systems. State diagrams require that the system is composed of a finite number of states. Sometimes, this is indeed the case, while at other times this is a reasonable abstraction. Many forms of state diagrams exist, which differ slightly and have different semantics.
In computer science, a deterministic algorithm is an algorithm that, given a particular input, will always produce the same output, with the underlying machine always passing through the same sequence of states. Deterministic algorithms are by far the most studied and familiar kind of algorithm, as well as one of the most practical, since they can be run on real machines efficiently.
Esterel is a synchronous programming language for the development of complex reactive systems. The imperative programming style of Esterel allows the simple expression of parallelism and preemption. As a consequence, it is well suited for control-dominated model designs.
Specification and Description Language (SDL) is a specification language targeted at the unambiguous specification and description of the behaviour of reactive and distributed systems.
Automata-based programming is a programming paradigm in which the program or part of it is thought of as a model of a finite-state machine (FSM) or any other formal automaton. Sometimes a potentially infinite set of possible states is introduced, and such a set can have a complicated structure, not just an enumeration.
The algorithmic state machine (ASM) is a method for designing finite state machines (FSMs) originally developed by Thomas E. Osborne at the University of California, Berkeley (UCB) since 1960, introduced to and implemented at Hewlett-Packard in 1968, formalized and expanded since 1967 and written about by Christopher R. Clare since 1970. It is used to represent diagrams of digital integrated circuits. The ASM diagram is like a state diagram but more structured and, thus, easier to understand. An ASM chart is a method of describing the sequential operations of a digital system.
In a conventional finite state machine, the transition is associated with a set of input Boolean conditions and a set of output Boolean functions. In an extended finite state machine (EFSM) model, the transition can be expressed by an “if statement” consisting of a set of trigger conditions. If trigger conditions are all satisfied, the transition is fired, bringing the machine from the current state to the next state and performing the specified data operations.
The Stream X-machine (SXM) is a model of computation introduced by Gilbert Laycock in his 1993 PhD thesis, The Theory and Practice of Specification Based Software Testing. Based on Samuel Eilenberg's X-machine, an extended finite-state machine for processing data of the type X, the Stream X-Machine is a kind of X-machine for processing a memory data type Mem with associated input and output streams In* and Out*, that is, where X = Out* × Mem × In*. The transitions of a Stream X-Machine are labelled by functions of the form φ: Mem × In → Out × Mem, that is, which compute an output value and update the memory, from the current memory and an input value.
The (Stream) X-Machine Testing Methodology is a complete functional testing approach to software- and hardware testing that exploits the scalability of the Stream X-Machine model of computation. Using this methodology, it is likely to identify a finite test-set that exhaustively determines whether the tested system's implementation matches its specification. This goal is achieved by a divide-and-conquer approach, in which the design is decomposed by refinement into a collection of Stream X-Machines, which are implemented as separate modules, then tested bottom-up. At each integration stage, the testing method guarantees that the tested components are correctly integrated.
Automata-based programming is a programming technology. Its defining characteristic is the use of finite state machines to describe program behavior. The transition graphs of state machines are used in all stages of software development. Automata-based programming technology was introduced by Anatoly Shalyto in 1991. Switch-technology was developed to support automata-based programming. Automata-based programming is considered to be rather general purpose program development methodology than just another one finite state machine implementation.

Control tables are tables that control the control flow or play a major part in program control. There are no rigid rules about the structure or content of a control table—its qualifying attribute is its ability to direct control flow in some way through "execution" by a processor or interpreter. The design of such tables is sometimes referred to as table-driven design. In some cases, control tables can be specific implementations of finite-state-machine-based automata-based programming. If there are several hierarchical levels of control table they may behave in a manner equivalent to UML state machines
Real-time Control System (RCS) is a reference model architecture, suitable for many software-intensive, real-time computing control problem domains. It defines the types of functions needed in a real-time intelligent control system, and how these functions relate to each other.
The Application Interface Specification (AIS) is a collection of open specifications that define the application programming interfaces (APIs) for high-availability application computer software. It is developed and published by the Service Availability Forum and made freely available. Besides reducing the complexity of high-availability applications and shortening development time, the specifications intended to ease the portability of applications between different middleware implementations and to admit third party developers to a field that was highly proprietary in the past.
Input/output automata provide a formal model, applicable in describing most types of an asynchronous concurrent system. On its own, the I/O automaton model contains a very basic structure that enables it to model various types of distributed systems. To describe specific types of asynchronous systems, additional structure must be added to this basic model. The model presents an explicit method for describing and reasoning about system components such as processes and message channels that interact with one another, operating at arbitrary relative speeds. The I/O automata were first introduced by Nancy A. Lynch and Mark R. Tuttle in "Hierarchical correctness proofs for distributed algorithms", 1987.
This glossary of computer science is a list of definitions of terms and concepts used in computer science, its sub-disciplines, and related fields, including terms relevant to software, data science, and computer programming.








