
A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules, crystals, and other structures. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing of electrons as in covalent bonds. The strength of chemical bonds varies considerably; there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force, and hydrogen bonding.

In physics, a dipole is an electromagnetic phenomenon which occurs in two ways:

A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.
Electrical resistivity is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). For example, if a 1 m3 solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as
Density-functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.
Electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either or . The density is determined, through definition, by the normalised -electron wavefunction which itself depends upon variables. Conversely, the density determines the wave function modulo up to a phase factor, providing the formal foundation of density functional theory.
In atomic physics, a partial charge is a non-integer charge value when measured in elementary charge units. It is represented by the Greek lowercase delta (𝛿), namely 𝛿− or 𝛿+.

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate energy levels and the resulting splittings in those energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.

In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current, permanent magnets, elementary particles, various molecules, and many astronomical objects.
In solid-state physics, the electronic band structure of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have.

Molecular modelling encompasses all methods, theoretical and computational, used to model or mimic the behaviour of molecules. The methods are used in the fields of computational chemistry, drug design, computational biology and materials science to study molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling methods is the atomistic level description of the molecular systems. This may include treating atoms as the smallest individual unit, or explicitly modelling protons and neutrons with its quarks, anti-quarks and gluons and electrons with its photons.
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons.

In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m−3), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m−2), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m−1), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative.
Ewald summation, named after Paul Peter Ewald, is a method for computing long-range interactions in periodic systems. It was first developed as the method for calculating the electrostatic energies of ionic crystals, and is now commonly used for calculating long-range interactions in computational chemistry. Ewald summation is a special case of the Poisson summation formula, replacing the summation of interaction energies in real space with an equivalent summation in Fourier space. In this method, the long-range interaction is divided into two parts: a short-range contribution, and a long-range contribution which does not have a singularity. The short-range contribution is calculated in real space, whereas the long-range contribution is calculated using a Fourier transform. The advantage of this method is the rapid convergence of the energy compared with that of a direct summation. This means that the method has high accuracy and reasonable speed when computing long-range interactions, and it is thus the de facto standard method for calculating long-range interactions in periodic systems. The method requires charge neutrality of the molecular system to accurately calculate the total Coulombic interaction. A study of the truncation errors introduced in the energy and force calculations of disordered point-charge systems is provided by Kolafa and Perram.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.

In physics, the atomic form factor, or atomic scattering factor, is a measure of the scattering amplitude of a wave by an isolated atom. The atomic form factor depends on the type of scattering, which in turn depends on the nature of the incident radiation, typically X-ray, electron or neutron. The common feature of all form factors is that they involve a Fourier transform of a spatial density distribution of the scattering object from real space to momentum space. For an object with spatial density distribution, , the form factor, , is defined as
The hybrid QM/MM approach is a molecular simulation method that combines the strengths of ab initio QM calculations (accuracy) and MM (speed) approaches, thus allowing for the study of chemical processes in solution and in proteins. The QM/MM approach was introduced in the 1976 paper of Warshel and Levitt. They, along with Martin Karplus, won the 2013 Nobel Prize in Chemistry for "the development of multiscale models for complex chemical systems".

In quantum chemistry, the electron localization function (ELF) is a measure of the likelihood of finding an electron in the neighborhood space of a reference electron located at a given point and with the same spin. Physically, this measures the extent of spatial localization of the reference electron and provides a method for the mapping of electron pair probability in multielectronic systems.
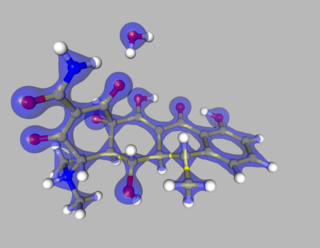
The Multipole Density Formalism is an X-ray crystallography method of electron density modelling proposed by Niels K. Hansen and Philip Coppens in 1978. Unlike the commonly used Independent Atom Model, the Hansen-Coppens Formalism presents an aspherical approach, allowing one to model the electron distribution around a nucleus separately in different directions and therefore describe numerous chemical features of a molecule inside the unit cell of an examined crystal in detail.









