Benford's law, also called the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading significant digit is likely to be small. For example, in sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use. Efficient multiplication algorithms have existed since the advent of the decimal system.
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it can be written as 3 × 3.

In mathematics, a power of two is a number of the form 2n where n is an integer, that is, the result of exponentiation with number two as the base and integer n as the exponent.

In arithmetic and algebra, the cube of a number n is its third power: the result of the number multiplied by itself twice:
A check digit is a form of redundancy check used for error detection on identification numbers, such as bank account numbers, which are used in an application where they will at least sometimes be input manually. It is analogous to a binary parity bit used to check for errors in computer-generated data. It consists of one or more digits computed by an algorithm from the other digits in the sequence input.
A happy number is defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits in base-ten, and repeat the process until the number either equals 1, or it loops endlessly in a cycle that does not include 1. Those numbers for which this process ends in 1 are happy numbers, while those that do not end in 1 are unhappy numbers.
Mental calculation comprises arithmetical calculations using only the human brain, with no help from any supplies or devices such as a calculator. People use mental calculation when computing tools are not available, when it is faster than other means of calculation, or even in a competitive context. Mental calculation often involves the use of specific techniques devised for specific types of problems. People with unusually high ability to perform mental calculations are called mental calculators or lightning calculators.
The Luhn algorithm or Luhn formula, also known as the "modulus 10" or "mod 10" algorithm, named after IBM scientist Hans Peter Luhn, is a simple checksum formula used to validate a variety of identification numbers, such as credit card numbers, IMEI numbers, National Provider Identifier numbers in the United States, Canadian Social Insurance Numbers, Israel ID Numbers, Greek Social Security Numbers (ΑΜΚΑ), and survey codes appearing on McDonald's, Taco Bell, and Tractor Supply Co. receipts. It was created by IBM scientist Hans Peter Luhn and described in U.S. Patent No. 2,950,048, filed on January 6, 1954, and granted on August 23, 1960.
In recreational mathematics, a harshad number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers in base n are also known as n-harshad numbers. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. The term “Niven number” arose from a paper delivered by Ivan M. Niven at a conference on number theory in 1977. All integers between zero and n are n-harshad numbers.
132 is the natural number following 131 and preceding 133.
A self number, Colombian number or Devlali number is an integer that cannot be written as the sum of any other integer n and the individual digits of n. This property is specific to the base used to represent the integers. 20 is a self number, because no such combination can be found. 21 is not, because it can be written as 15 + 1 + 5 using n = 15.
A divisibility rule is a shorthand way of determining whether a given integer is divisible by a fixed divisor without performing the division, usually by examining its digits. Although there are divisibility tests for numbers in any radix, or base, and they are all different, this article presents rules and examples only for decimal, or base 10, numbers. Martin Gardner explained and popularized these rules in his September 1962 "Mathematical Games" column in Scientific American.
Significance arithmetic is a set of rules for approximating the propagation of uncertainty in scientific or statistical calculations. These rules can be used to find the appropriate number of significant figures to use to represent the result of a calculation. If a calculation is done without analysis of the uncertainty involved, a result that is written with too many significant figures can be taken to imply a higher precision than is known, and a result that is written with too few significant figures results in an avoidable loss of precision. Understanding these rules requires a good understanding of the concept of significant and insignificant figures.
A cyclic number is an integer in which cyclic permutations of the digits are successive multiples of the number. The most widely known is the six-digit number 142857, whose first six integer multiples are
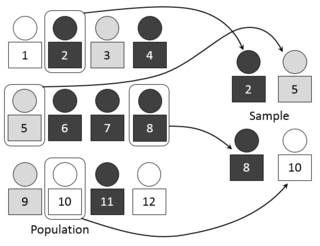
The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used to compare two related samples, matched samples, or repeated measurements on a single sample to assess whether their population mean ranks differ. It can be used as an alternative to the paired Student's t-test when the population cannot be assumed to be normally distributed. A Wilcoxon signed-rank test is a nonparametric test that can be used to determine whether two dependent samples were selected from populations having the same distribution.
In recreational number theory, a narcissistic number is a number that is the sum of its own digits each raised to the power of the number of digits. This definition depends on the base b of the number system used, e.g., b = 10 for the decimal system or b = 2 for the binary system.
A sum-product number is an integer that in a given base is equal to the sum of its digits times the product of its digits. Or, to put it algebraically, given an integer n that is l digits long in base b, if:
The digital root of a non-negative integer is the value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached.
Missing-digit sums are integer numbers that are equal to the sum of numbers created by deleting one or more digits at a time from the original number. For example, the OEIS lists these two integers as missing-digit sums in base ten: