Motzkin number

Motzkin number
Named after	Theodore Motzkin
Publication year	1948
Author of publication	Theodore Motzkin
No. of known terms	infinity
Formula	see Properties
First terms	1, 1, 2, 4, 9, 21, 51
OEIS index	A001006 ; Motzkin;

Last updated April 19, 2024

In mathematics, the $n$ th Motzkin number is the number of different ways of drawing non-intersecting chords between $n$ points on a circle (not necessarily touching every point by a chord). The Motzkin numbers are named after Theodore Motzkin and have diverse applications in geometry, combinatorics and number theory.

Examples

The following figure shows the 9 ways to draw non-intersecting chords between 4 points on a circle ( $M 4 = 9$ ):

The following figure shows the 21 ways to draw non-intersecting chords between 5 points on a circle ( $M 5 = 21$ ):

Properties

The Motzkin numbers satisfy the recurrence relations

M_{n}=M_{n-1}+\sum _{i=0}^{n-2}M_{i}M_{n-2-i}={\frac {2n+1}{n+2}}M_{n-1}+{\frac {3n-3}{n+2}}M_{n-2}.

The Motzkin numbers can be expressed in terms of binomial coefficients and Catalan numbers:

M_{n}=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}C_{k},

and inversely,^[1]

C_{n+1}=\sum _{k=0}^{n}{\binom {n}{k}}M_{k}

This gives

\sum _{k=0}^{n}C_{k}=1+\sum _{k=1}^{n}{\binom {n}{k}}M_{k-1}.

The generating function $m(x)=\sum _{n=0}^{\infty }M_{n}x^{n}$ of the Motzkin numbers satisfies

x^{2}m(x)^{2}+(x-1)m(x)+1=0

and is explicitly expressed as

m(x)={\frac {1-x-{\sqrt {1-2x-3x^{2}}}}{2x^{2}}}.

An integral representation of Motzkin numbers is given by

M_{n}={\frac {2}{\pi }}\int _{0}^{\pi }\sin(x)^{2}(2\cos(x)+1)^{n}dx

.

They have the asymptotic behaviour

M_{n}\sim {\frac {1}{2{\sqrt {\pi }}}}\left({\frac {3}{n}}\right)^{3/2}3^{n},~n\to \infty

.

A Motzkin prime is a Motzkin number that is prime. As of 2019^[update], only four such primes are known:

2, 127, 15511, 953467954114363 (sequence A092832 in the OEIS )

Combinatorial interpretations

The Motzkin number for $n$ is also the number of positive integer sequences of length $n - 1$ in which the opening and ending elements are either 1 or 2, and the difference between any two consecutive elements is −1, 0 or 1. Equivalently, the Motzkin number for $n$ is the number of positive integer sequences of length $n + 1$ in which the opening and ending elements are 1, and the difference between any two consecutive elements is −1, 0 or 1.

Also, the Motzkin number for $n$ gives the number of routes on the upper right quadrant of a grid from coordinate (0, 0) to coordinate ( $n$ , 0) in $n$ steps if one is allowed to move only to the right (up, down or straight) at each step but forbidden from dipping below the $y$ = 0 axis.

For example, the following figure shows the 9 valid Motzkin paths from (0, 0) to (4, 0):

There are at least fourteen different manifestations of Motzkin numbers in different branches of mathematics, as enumerated by Donaghey & Shapiro (1977) in their survey of Motzkin numbers. Guibert, Pergola & Pinzani (2001) showed that vexillary involutions are enumerated by Motzkin numbers.

Related Research Articles

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n; this coefficient can be computed by the multiplicative formula$

In mathematics, the Bernoulli numbers $B n$ are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by $or, is equal to the binomial coefficient$

In mathematics, the Euler numbers are a sequence E_n of integers defined by the Taylor series expansion

In mathematics, Stirling numbers arise in a variety of analytic and combinatorial problems. They are named after James Stirling, who introduced them in a purely algebraic setting in his book Methodus differentialis (1730). They were rediscovered and given a combinatorial meaning by Masanobu Saka in 1782.

In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.

In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Catalan.

In mathematics, the falling factorial is defined as the polynomial

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the number of stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.

In mathematics, Apéry's theorem is a result in number theory that states the Apéry's constant ζ(3) is irrational. That is, the number

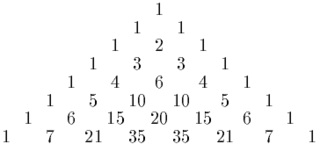
In mathematics the nth central binomial coefficient is the particular binomial coefficient

In mathematics, particularly in combinatorics, a Stirling number of the second kind is the number of ways to partition a set of n objects into k non-empty subsets and is denoted by $or . Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions. They are named after James Stirling.$

<span class="mw-page-title-main">Ordered Bell number</span> Number of weak orderings

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of $elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race. Starting from, these numbers are$

In mathematics, a Delannoy number $describes the number of paths from the southwest corner (0, 0) of a rectangular grid to the northeast corner (m, n), using only single steps north, northeast, or east. The Delannoy numbers are named after French army officer and amateur mathematician Henri Delannoy.$

In mathematics, the Schröder number $also called a large Schröder number or big Schröder number, describes the number of lattice paths from the southwest corner of an grid to the northeast corner using only single steps north, northeast, or east, that do not rise above the SW-NE diagonal.$

In mathematics, a vexillary permutation is a permutation μ of the positive integers containing no subpermutation isomorphic to the permutation (2143); in other words, there do not exist four numbers i < j < k < l with μ(j) < μ(i) < μ(l) < μ(k). They were introduced by Lascoux and Schützenberger (1982, 1985). The word "vexillary" means flag-like, and comes from the fact that vexillary permutations are related to flags of modules.

In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways $n$ people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings of a complete graph on $n$ vertices, the number of permutations on $n$ elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with $n$ cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values

In mathematics, a transformation of a sequence's generating function provides a method of converting the generating function for one sequence into a generating function enumerating another. These transformations typically involve integral formulas applied to a sequence generating function or weighted sums over the higher-order derivatives of these functions.

References

↑ Yi Wang and Zhi-Hai Zhang (2015). "Combinatorics of Generalized Motzkin Numbers" (PDF). Journal of Integer Sequences (18).

Bernhart, Frank R. (1999), "Catalan, Motzkin, and Riordan numbers", Discrete Mathematics , 204 (1–3): 73–112, doi: 10.1016/S0012-365X(99)00054-0
Donaghey, R.; Shapiro, L. W. (1977), "Motzkin numbers", Journal of Combinatorial Theory , Series A, 23 (3): 291–301, doi: 10.1016/0097-3165(77)90020-6 , MR 0505544
Guibert, O.; Pergola, E.; Pinzani, R. (2001), "Vexillary involutions are enumerated by Motzkin numbers", Annals of Combinatorics , 5 (2): 153–174, doi:10.1007/PL00001297, ISSN 0218-0006, MR 1904383, S2CID 123053532
Motzkin, T. S. (1948), "Relations between hypersurface cross ratios, and a combinatorial formula for partitions of a polygon, for permanent preponderance, and for non-associative products", Bulletin of the American Mathematical Society , 54 (4): 352–360, doi: 10.1090/S0002-9904-1948-09002-4

External links

Weisstein, Eric W. "Motzkin Number". MathWorld .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Yi Wang and Zhi-Hai Zhang (2015). "Combinatorics of Generalized Motzkin Numbers" (PDF). Journal of Integer Sequences (18).

[1]