Aliquot sequence

Last updated September 25, 2023

Definition and overview

The aliquot sequence starting with a positive integer $k$ can be defined formally in terms of the sum-of-divisors function $σ 1$ or the aliquot sum function $s$ in the following way:^[1]

{\begin{aligned}s_{0}&=k\\[4pt]s_{n}&=s(s_{n-1})=\sigma _{1}(s_{n-1})-s_{n-1}\quad {\text{if}}\quad s_{n-1}>0\\[4pt]s_{n}&=0\quad {\text{if}}\quad s_{n-1}=0\\[4pt]s(0)&={\text{undefined}}\end{aligned}}

If the $s n -1 = 0$ condition is added, then the terms after 0 are all 0, and all aliquot sequences would be infinite, and we can conjecture that all aliquot sequences are convergent, the limit of these sequences are usually 0 or 6.

For example, the aliquot sequence of 10 is 10, 8, 7, 1, 0 because:

{\begin{aligned}\sigma _{1}(10)-10&=5+2+1=8,\\[4pt]\sigma _{1}(8)-8&=4+2+1=7,\\[4pt]\sigma _{1}(7)-7&=1,\\[4pt]\sigma _{1}(1)-1&=0.\end{aligned}}

Many aliquot sequences terminate at zero; all such sequences necessarily end with a prime number followed by 1 (since the only proper divisor of a prime is 1), followed by 0 (since 1 has no proper divisors). See (sequence A080907 in the OEIS ) for a list of such numbers up to 75. There are a variety of ways in which an aliquot sequence might not terminate:

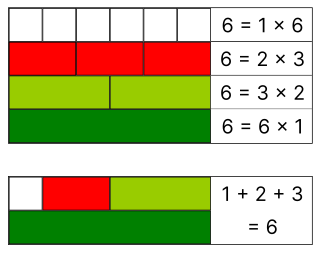
A perfect number has a repeating aliquot sequence of period 1. The aliquot sequence of 6, for example, is 6, 6, 6, 6, ...
An amicable number has a repeating aliquot sequence of period 2. For instance, the aliquot sequence of 220 is 220, 284, 220, 284, ...
A sociable number has a repeating aliquot sequence of period 3 or greater. (Sometimes the term sociable number is used to encompass amicable numbers as well.) For instance, the aliquot sequence of 1264460 is 1264460, 1547860, 1727636, 1305184, 1264460, ...
Some numbers have an aliquot sequence which is eventually periodic, but the number itself is not perfect, amicable, or sociable. For instance, the aliquot sequence of 95 is 95, 25, 6, 6, 6, 6, ... Numbers like 95 that are not perfect, but have an eventually repeating aliquot sequence of period 1 are called aspiring numbers.^[2]

Aliquot sequences from 0 to 47
$n$	Aliquot sequence of $n$	Length ( OEIS: A098007 )
0	0	1
1	1, 0	2
2	2, 1, 0	3
3	3, 1, 0	3
4	4, 3, 1, 0	4
5	5, 1, 0	3
6	6	1
7	7, 1, 0	3
8	8, 7, 1, 0	4
9	9, 4, 3, 1, 0	5
10	10, 8, 7, 1, 0	5
11	11, 1, 0	3
12	12, 16, 15, 9, 4, 3, 1, 0	8
13	13, 1, 0	3
14	14, 10, 8, 7, 1, 0	6
15	15, 9, 4, 3, 1, 0	6
16	16, 15, 9, 4, 3, 1, 0	7
17	17, 1, 0	3
18	18, 21, 11, 1, 0	5
19	19, 1, 0	3
20	20, 22, 14, 10, 8, 7, 1, 0	8
21	21, 11, 1, 0	4
22	22, 14, 10, 8, 7, 1, 0	7
23	23, 1, 0	3
24	24, 36, 55, 17, 1, 0	6
25	25, 6	2
26	26, 16, 15, 9, 4, 3, 1, 0	8
27	27, 13, 1, 0	4
28	28	1
29	29, 1, 0	3
30	30, 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0	16
31	31, 1, 0	3
32	32, 31, 1, 0	4
33	33, 15, 9, 4, 3, 1, 0	7
34	34, 20, 22, 14, 10, 8, 7, 1, 0	9
35	35, 13, 1, 0	4
36	36, 55, 17, 1, 0	5
37	37, 1, 0	3
38	38, 22, 14, 10, 8, 7, 1, 0	8
39	39, 17, 1, 0	4
40	40, 50, 43, 1, 0	5
41	41, 1, 0	3
42	42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0	15
43	43, 1, 0	3
44	44, 40, 50, 43, 1, 0	6
45	45, 33, 15, 9, 4, 3, 1, 0	8
46	46, 26, 16, 15, 9, 4, 3, 1, 0	9
47	47, 1, 0	3

The lengths of the aliquot sequences that start at $n$ are

1, 2, 2, 3, 2, 1, 2, 3, 4, 4, 2, 7, 2, 5, 5, 6, 2, 4, 2, 7, 3, 6, 2, 5, 1, 7, 3, 1, 2, 15, 2, 3, 6, 8, 3, 4, 2, 7, 3, 4, 2, 14, 2, 5, 7, 8, 2, 6, 4, 3, ... (sequence A044050 in the OEIS )

The final terms (excluding 1) of the aliquot sequences that start at $n$ are

1, 2, 3, 3, 5, 6, 7, 7, 3, 7, 11, 3, 13, 7, 3, 3, 17, 11, 19, 7, 11, 7, 23, 17, 6, 3, 13, 28, 29, 3, 31, 31, 3, 7, 13, 17, 37, 7, 17, 43, 41, 3, 43, 43, 3, 3, 47, 41, 7, 43, ... (sequence A115350 in the OEIS )

Numbers whose aliquot sequence terminates in 1 are

1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, ... (sequence A080907 in the OEIS )

Numbers whose aliquot sequence known to terminate in a perfect number, other than perfect numbers themselves (6, 28, 496, ...), are

25, 95, 119, 143, 417, 445, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913, ... (sequence A063769 in the OEIS )

Numbers whose aliquot sequence terminates in a cycle with length at least 2 are

220, 284, 562, 1064, 1184, 1188, 1210, 1308, 1336, 1380, 1420, 1490, 1604, 1690, 1692, 1772, 1816, 1898, 2008, 2122, 2152, 2172, 2362, ... (sequence A121507 in the OEIS )

Numbers whose aliquot sequence is not known to be finite or eventually periodic are

276, 306, 396, 552, 564, 660, 696, 780, 828, 888, 966, 996, 1074, 1086, 1098, 1104, 1134, 1218, 1302, 1314, 1320, 1338, 1350, 1356, 1392, 1398, 1410, 1464, 1476, 1488, ... (sequence A131884 in the OEIS )

A number that is never the successor in an aliquot sequence is called an untouchable number.

2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448, 472, 474, 498, ... (sequence A005114 in the OEIS )

Catalan–Dickson conjecture

An important conjecture due to Catalan, sometimes called the Catalan–Dickson conjecture, is that every aliquot sequence ends in one of the above ways: with a prime number, a perfect number, or a set of amicable or sociable numbers.^[3] The alternative would be that a number exists whose aliquot sequence is infinite yet never repeats. Any one of the many numbers whose aliquot sequences have not been fully determined might be such a number. The first five candidate numbers are often called the Lehmer five (named after D.H. Lehmer): 276, 552, 564, 660, and 966.^[4] However, it is worth noting that 276 may reach a high apex in its aliquot sequence and then descend; the number 138 reaches a peak of 179931895322 before returning to 1.

Guy and Selfridge believe the Catalan–Dickson conjecture is false (so they conjecture some aliquot sequences are unbounded above (i.e., diverge)).^[5]

As of April 2015^[update], there were 898 positive integers less than 100,000 whose aliquot sequences have not been fully determined, and 9190 such integers less than 1,000,000.^[6]

Systematically searching for aliquot sequences

The aliquot sequence can be represented as a directed graph, $G_{n,s}$ , for a given integer $n$ , where $s(k)$ denotes the sum of the proper divisors of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): k.^[7] Cycles in $G_{n,s}$ represent sociable numbers within the interval $[1,n]$ . Two special cases are loops that represent perfect numbers and cycles of length two that represent amicable pairs.

Notes

↑ Weisstein, Eric W. "Aliquot Sequence". MathWorld .
↑ Sloane, N. J. A. (ed.). "SequenceA063769(Aspiring numbers: numbers whose aliquot sequence terminates in a perfect number.)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.
↑ Weisstein, Eric W. "Catalan's Aliquot Sequence Conjecture". MathWorld .
↑ Creyaufmüller, Wolfgang (May 24, 2014). "Lehmer Five" . Retrieved June 14, 2015.
↑ A. S. Mosunov, What do we know about aliquot sequences?
↑ Creyaufmüller, Wolfgang (April 29, 2015). "Aliquot Pages" . Retrieved June 14, 2015.
↑ Rocha, Rodrigo Caetano; Thatte, Bhalchandra (2015), Distributed cycle detection in large-scale sparse graphs, Simpósio Brasileiro de Pesquisa Operacional (SBPO), doi:10.13140/RG.2.1.1233.8640

Related Research Articles

Amicable numbers are two different natural numbers related in such a way that the sum of the proper divisors of each is equal to the other number. That is, s(a)=b and s(b)=a, where s(n)=σ(n)-n is equal to the sum of positive divisors of n except n itself (see also divisor function).

In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number.

45 (forty-five) is the natural number following 44 and preceding 46.

In number theory, an abundant number or excessive number is a positive integer for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.

In number theory, a deficient number or defective number is a positive integer $n$ for which the sum of divisors of $n$ is less than $2 n$ . Equivalently, it is a number for which the sum of proper divisors is less than $n$ . For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient.

In mathematics, sociable numbers are numbers whose aliquot sums form a periodic sequence. They are generalizations of the concepts of perfect numbers and amicable numbers. The first two sociable sequences, or sociable chains, were discovered and named by the Belgian mathematician Paul Poulet in 1918. In a sociable sequence, each number is the sum of the proper divisors of the preceding number, i.e., the sum excludes the preceding number itself. For the sequence to be sociable, the sequence must be cyclic and return to its starting point.

63 (sixty-three) is the natural number following 62 and preceding 64.

<span class="mw-page-title-main">Divisor function</span> Arithmetic function related to the divisors of an integer

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

In mathematics, a harmonic divisor number, or Ore number, is a positive integer whose divisors have a harmonic mean that is an integer. The first few harmonic divisor numbers are:

In mathematics, an untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer. That is, these numbers are not in the image of the aliquot sum function. Their study goes back at least to Abu Mansur al-Baghdadi, who observed that both 2 and 5 are untouchable.

In number theory, a practical number or panarithmic number is a positive integer $such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.$

The Ramanujan tau function, studied by Ramanujan (1916), is the function $:\mathbb {N} \rightarrow \mathbb {Z} }$ defined by the following identity:

In number theory, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it is defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.

In number theory, friendly numbers are two or more natural numbers with a common abundancy index, the ratio between the sum of divisors of a number and the number itself. Two numbers with the same "abundancy" form a friendly pair; n numbers with the same "abundancy" form a friendly n-tuple.

In mathematics, a natural number a is a unitary divisor of a number b if a is a divisor of b and if a and $are coprime, having no common factor other than 1. Thus, 5 is a unitary divisor of 60, because 5 and have only 1 as a common factor, while 6 is a divisor but not a unitary divisor of 60, as 6 and have a common factor other than 1, namely 2. 1 is a unitary divisor of every natural number.$

252 is the natural number following 251 and preceding 253.

744 is the natural number following 743 and preceding 745.

In number theory, the aliquot sums(n) of a positive integer n is the sum of all proper divisors of n, that is, all divisors of n other than n itself. That is,

In mathematics, a superperfect number is a positive integer n that satisfies

Betrothed numbers or quasi-amicable numbers are two positive integers such that the sum of the proper divisors of either number is one more than the value of the other number. In other words, (m, n) are a pair of betrothed numbers if s(m) = n + 1 and s(n) = m + 1, where s(n) is the aliquot sum of n: an equivalent condition is that σ(m) = σ(n) = m + n + 1, where σ denotes the sum-of-divisors function.

References

Manuel Benito; Wolfgang Creyaufmüller; Juan Luis Varona; Paul Zimmermann. Aliquot Sequence 3630 Ends After Reaching 100 Digits. Experimental Mathematics, vol. 11, num. 2, Natick, MA, 2002, p. 201–206.
W. Creyaufmüller. Primzahlfamilien - Das Catalan'sche Problem und die Familien der Primzahlen im Bereich 1 bis 3000 im Detail. Stuttgart 2000 (3rd ed.), 327p.

External links

Current status of aliquot sequences with start term below 2 million
Tables of Aliquot Cycles (J.O.M. Pedersen)
Aliquot Page (Wolfgang Creyaufmüller)
Aliquot sequences (Christophe Clavier)
Forum on calculating aliquot sequences (MersenneForum)
Aliquot sequence summary page for sequences up to 100000 (there are similar pages for higher ranges) (Karsten Bonath)
Active research site on aliquot sequences (Jean-Luc Garambois) (in French)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[mw-1] Weisstein, Eric W. "Aliquot Sequence". MathWorld .

[2] Sloane, N. J. A. (ed.). "SequenceA063769(Aspiring numbers: numbers whose aliquot sequence terminates in a perfect number.)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.

[3] Weisstein, Eric W. "Catalan's Aliquot Sequence Conjecture". MathWorld .

[4] Creyaufmüller, Wolfgang (May 24, 2014). "Lehmer Five" . Retrieved June 14, 2015.

[5] A. S. Mosunov, What do we know about aliquot sequences?

[6] Creyaufmüller, Wolfgang (April 29, 2015). "Aliquot Pages" . Retrieved June 14, 2015.

[7] Rocha, Rodrigo Caetano; Thatte, Bhalchandra (2015), Distributed cycle detection in large-scale sparse graphs, Simpósio Brasileiro de Pesquisa Operacional (SBPO), doi:10.13140/RG.2.1.1233.8640

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v t e Divisibility-based sets of integers
Overview	Integer factorization Divisor Unitary divisor Divisor function Prime factor Fundamental theorem of arithmetic
Factorization forms	Prime Composite Semiprime Pronic Sphenic Square-free Powerful Perfect power Achilles Smooth Regular Rough Unusual
Constrained divisor sums	Perfect Almost perfect Quasiperfect Multiply perfect Hemiperfect Hyperperfect Superperfect Unitary perfect Semiperfect Practical Erdős–Nicolas
With many divisors	Abundant Primitive abundant Highly abundant Superabundant Colossally abundant Highly composite Superior highly composite Weird
Aliquot sequence-related	Untouchable Amicable (Triple) Sociable Betrothed
Base-dependent	Equidigital Extravagant Frugal Harshad Polydivisible Smith
Other sets	Arithmetic Deficient Friendly Solitary Sublime Harmonic divisor Descartes Refactorable Superperfect