In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n; this coefficient can be computed by the multiplicative formula
In mathematics, the Bernoulli numbersBn are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,
In mathematics, the Euler numbers are a sequence En of integers defined by the Taylor series expansion
In mathematics, Stirling numbers arise in a variety of analytic and combinatorial problems. They are named after James Stirling, who introduced them in a purely algebraic setting in his book Methodus differentialis (1730). They were rediscovered and given a combinatorial meaning by Masanobu Saka in 1782.

In mathematics, Stirling's approximation is an asymptotic approximation for factorials. It is a good approximation, leading to accurate results even for small values of . It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre.
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:
In mathematics, the falling factorial is defined as the polynomial

In mathematics, the double factorial of a number n, denoted by n‼, is the product of all the positive integers up to n that have the same parity as n. That is,
In probability theory, the factorial moment is a mathematical quantity defined as the expectation or average of the falling factorial of a random variable. Factorial moments are useful for studying non-negative integer-valued random variables, and arise in the use of probability-generating functions to derive the moments of discrete random variables.

In mathematics, the Laguerre polynomials, named after Edmond Laguerre (1834–1886), are nontrivial solutions of Laguerre's differential equation:
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence defines a series S that is denoted

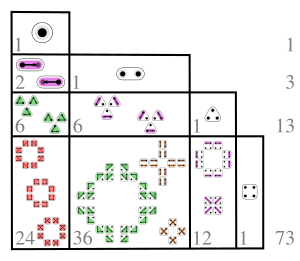
In mathematics, particularly in combinatorics, a Stirling number of the second kind is the number of ways to partition a set of n objects into k non-empty subsets and is denoted by or . Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions. They are named after James Stirling.
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.
In mathematics, the Stirling polynomials are a family of polynomials that generalize important sequences of numbers appearing in combinatorics and analysis, which are closely related to the Stirling numbers, the Bernoulli numbers, and the generalized Bernoulli polynomials. There are multiple variants of the Stirling polynomial sequence considered below most notably including the Sheffer sequence form of the sequence, , defined characteristically through the special form of its exponential generating function, and the Stirling (convolution) polynomials, , which also satisfy a characteristic ordinary generating function and that are of use in generalizing the Stirling numbers to arbitrary complex-valued inputs. We consider the "convolution polynomial" variant of this sequence and its properties second in the last subsection of the article. Still other variants of the Stirling polynomials are studied in the supplementary links to the articles given in the references.

In combinatorics, the Eulerian number is the number of permutations of the numbers 1 to in which exactly elements are greater than the previous element.
In the mathematical theory of special functions, the Pochhammer k-symbol and the k-gamma function, introduced by Rafael Díaz and Eddy Pariguan are generalizations of the Pochhammer symbol and gamma function. They differ from the Pochhammer symbol and gamma function in that they can be related to a general arithmetic progression in the same manner as those are related to the sequence of consecutive integers.
In mathematics, a Carleman matrix is a matrix used to convert function composition into matrix multiplication. It is often used in iteration theory to find the continuous iteration of functions which cannot be iterated by pattern recognition alone. Other uses of Carleman matrices occur in the theory of probability generating functions, and Markov chains.
In mathematics, a transformation of a sequence's generating function provides a method of converting the generating function for one sequence into a generating function enumerating another. These transformations typically involve integral formulas applied to a sequence generating function or weighted sums over the higher-order derivatives of these functions.