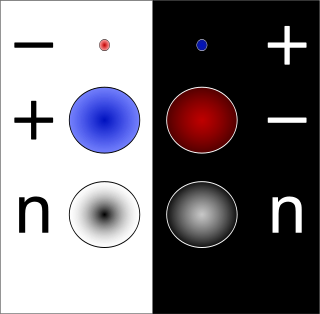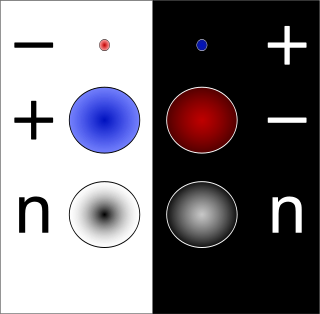
In particle physics, every type of particle of "ordinary" matter is associated with an antiparticle with the same mass but with opposite physical charges. For example, the antiparticle of the electron is the positron. While the electron has a negative electric charge, the positron has a positive electric charge, and is produced naturally in certain types of radioactive decay. The opposite is also true: the antiparticle of the positron is the electron.
In quantum mechanics, indistinguishable particles are particles that cannot be distinguished from one another, even in principle. Species of identical particles include, but are not limited to, elementary particles, composite subatomic particles, as well as atoms and molecules. Quasiparticles also behave in this way. Although all known indistinguishable particles only exist at the quantum scale, there is no exhaustive list of all possible sorts of particles nor a clear-cut limit of applicability, as explored in quantum statistics. They were first discussed by Werner Heisenberg and Paul Dirac in 1926.
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, which are a kind of linear space. Such are distinguished from mathematical formalisms for physics theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces, and operators on these spaces. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely as spectral values of linear operators in Hilbert space.

In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940.

The Zeeman effect is the effect of splitting of a spectral line into several components in the presence of a static magnetic field. It is named after the Dutch physicist Pieter Zeeman, who discovered it in 1896 and received a Nobel prize for this discovery. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field. Also similar to the Stark effect, transitions between different components have, in general, different intensities, with some being entirely forbidden, as governed by the selection rules.
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles. These states are named after the Soviet physicist Vladimir Fock. Fock states play an important role in the second quantization formulation of quantum mechanics.
In quantum mechanics, a Slater determinant is an expression that describes the wave function of a multi-fermionic system. It satisfies anti-symmetry requirements, and consequently the Pauli principle, by changing sign upon exchange of two electrons. Only a small subset of all possible fermionic wave functions can be written as a single Slater determinant, but those form an important and useful subset because of their simplicity.

In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant.
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
In magnetism, the Curie–Weiss law describes the magnetic susceptibility χ of a ferromagnet in the paramagnetic region above the Curie temperature:

Quantum orbital motion involves the quantum mechanical motion of rigid particles about some other mass, or about themselves. In classical mechanics, an object's orbital motion is characterized by its orbital angular momentum and spin angular momentum, which is the object's angular momentum about its own center of mass. In quantum mechanics there are analogous orbital and spin angular momenta which describe the orbital motion of a particle, represented as quantum mechanical operators instead of vectors.
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi–Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields.

In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the degree of degeneracy of the level. It is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy.
In quantum mechanics, the exchange operator, also known as permutation operator, is a quantum mechanical operator that acts on states in Fock space. The exchange operator acts by switching the labels on any two identical particles described by the joint position quantum state . Since the particles are identical, the notion of exchange symmetry requires that the exchange operator be unitary.
The Bose–Hubbard model gives a description of the physics of interacting spinless bosons on a lattice. It is closely related to the Hubbard model that originated in solid-state physics as an approximate description of superconducting systems and the motion of electrons between the atoms of a crystalline solid. The model was introduced by Gersch and Knollman in 1963 in the context of granular superconductors. The model rose to prominence in the 1980s after it was found to capture the essence of the superfluid-insulator transition in a way that was much more mathematically tractable than fermionic metal-insulator models.
In quantum mechanics, a raising or lowering operator is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raising operator is sometimes called the creation operator, and the lowering operator the annihilation operator. Well-known applications of ladder operators in quantum mechanics are in the formalisms of the quantum harmonic oscillator and angular momentum.
In quantum mechanics and quantum field theory, a Schrödinger field, named after Erwin Schrödinger, is a quantum field which obeys the Schrödinger equation. While any situation described by a Schrödinger field can also be described by a many-body Schrödinger equation for identical particles, the field theory is more suitable for situations where the particle number changes.
Spin is an intrinsic form of angular momentum carried by elementary particles, and thus by composite particles such as hadrons, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory.
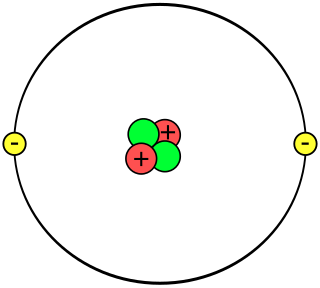
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927. Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.
This is a glossary for the terminology often encountered in undergraduate quantum mechanics courses.