The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842-1850 (Stokes).

In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero.

Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.

In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.
In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.

The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.

In fluid mechanics and hydraulics, open-channel flow is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways but differ in one important respect: open-channel flow has a free surface, whereas pipe flow does not.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.
In fluid dynamics, dynamic pressure is the quantity defined by:
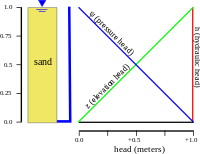
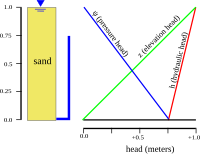
In fluid mechanics, pressure head is the height of a liquid column that corresponds to a particular pressure exerted by the liquid column on the base of its container. It may also be called static pressure head or simply static head.
In fluid dynamics, total dynamic head (TDH) is the work to be done by a pump, per unit weight, per unit volume of fluid. TDH is expressed as the total equivalent height that a fluid is to be pumped, taking into account friction losses in the pipe.
In plasma physics, the Hasegawa–Mima equation, named after Akira Hasegawa and Kunioki Mima, is an equation that describes a certain regime of plasma, where the time scales are very fast, and the distance scale in the direction of the magnetic field is long. In particular the equation is useful for describing turbulence in some tokamaks. The equation was introduced in Hasegawa and Mima's paper submitted in 1977 to Physics of Fluids, where they compared it to the results of the ATC tokamak.

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.

HydroGeoSphere (HGS) is a 3D control-volume finite element groundwater model, and is based on a rigorous conceptualization of the hydrologic system consisting of surface and subsurface flow regimes. The model is designed to take into account all key components of the hydrologic cycle. For each time step, the model solves surface and subsurface flow, solute and energy transport equations simultaneously, and provides a complete water and solute balance.
In theoretical physics, the Madelung equations, or the equations of quantum hydrodynamics, are Erwin Madelung's equivalent alternative formulation of the Schrödinger equation, written in terms of hydrodynamical variables, similar to the Navier–Stokes equations of fluid dynamics. The derivation of the Madelung equations is similar to the de Broglie–Bohm formulation, which represents the Schrödinger equation as a quantum Hamilton–Jacobi equation.
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.
In fluid dynamics the Borda–Carnot equation is an empirical description of the mechanical energy losses of the fluid due to a (sudden) flow expansion. It describes how the total head reduces due to the losses. This is in contrast with Bernoulli's principle for dissipationless flow, where the total head is a constant along a streamline. The equation is named after Jean-Charles de Borda (1733–1799) and Lazare Carnot (1753–1823).
In fluid dynamics, Hicks equation or sometimes also referred as Bragg–Hawthorne equation or Squire–Long equation is a partial differential equation that describes the distribution of stream function for axisymmetric inviscid fluid, named after William Mitchinson Hicks, who derived it first in 1898. The equation was also re-derived by Stephen Bragg and William Hawthorne in 1950 and by Robert R. Long in 1953 and by Herbert Squire in 1956. The Hicks equation without swirl was first introduced by George Gabriel Stokes in 1842. The Grad–Shafranov equation appearing in plasma physics also takes the same form as the Hicks equation.