In-place algorithm

Last updated June 23, 2023

In computer science, an in-place algorithm is an algorithm that operates directly on the input data structure without requiring extra space proportional to the input size. In other words, it modifies the input in place, without creating a separate copy of the data structure. An algorithm which is not in-place is sometimes called not-in-place or out-of-place.

In-place can have slightly different meanings. In its strictest form, the algorithm can only have a constant amount of extra space, counting everything including function calls and pointers. However, this form is very limited as simply having an index to a length $n$ array requires $O (log n)$ bits. More broadly, in-place means that the algorithm does not use extra space for manipulating the input but may require a small though nonconstant extra space for its operation. Usually, this space is $O (log n)$ , though sometimes anything in $o (n)$ is allowed. Note that space complexity also has varied choices in whether or not to count the index lengths as part of the space used. Often, the space complexity is given in terms of the number of indices or pointers needed, ignoring their length. In this article, we refer to total space complexity (DSPACE), counting pointer lengths. Therefore, the space requirements here have an extra $log n$ factor compared to an analysis that ignores the length of indices and pointers.

An algorithm may or may not count the output as part of its space usage. Since in-place algorithms usually overwrite their input with output, no additional space is needed. When writing the output to write-only memory or a stream, it may be more appropriate to only consider the working space of the algorithm. In theoretical applications such as log-space reductions, it is more typical to always ignore output space (in these cases it is more essential that the output is write-only).

Examples

Given an array a of $n$ items, suppose we want an array that holds the same elements in reversed order and to dispose of the original. One seemingly simple way to do this is to create a new array of equal size, fill it with copies from a in the appropriate order and then delete a.

function reverse(a[0..n - 1])      allocate b[0..n - 1]      for i from 0 to n - 1          b[n − 1 − i] := a[i]      return b

Unfortunately, this requires $O (n)$ extra space for having the arrays a and b available simultaneously. Also, allocation and deallocation are often slow operations. Since we no longer need a, we can instead overwrite it with its own reversal using this in-place algorithm which will only need constant number (2) of integers for the auxiliary variables i and tmp, no matter how large the array is.

function reverse_in_place(a[0..n-1])      for i from 0 to floor((n-2)/2)          tmp := a[i]          a[i] := a[n − 1 − i]          a[n − 1 − i] := tmp

As another example, many sorting algorithms rearrange arrays into sorted order in-place, including: bubble sort, comb sort, selection sort, insertion sort, heapsort, and Shell sort. These algorithms require only a few pointers, so their space complexity is $O (log n)$ .^[1]

Quicksort operates in-place on the data to be sorted. However, quicksort requires $O (log n)$ stack space pointers to keep track of the subarrays in its divide and conquer strategy. Consequently, quicksort needs $O (log 2 n)$ additional space. Although this non-constant space technically takes quicksort out of the in-place category, quicksort and other algorithms needing only $O (log n)$ additional pointers are usually considered in-place algorithms.

Most selection algorithms are also in-place, although some considerably rearrange the input array in the process of finding the final, constant-sized result.

Some text manipulation algorithms such as trim and reverse may be done in-place.

In computational complexity

In computational complexity theory, the strict definition of in-place algorithms includes all algorithms with $O (1)$ space complexity, the class DSPACE (1). This class is very limited; it equals the regular languages.^[2] In fact, it does not even include any of the examples listed above.

Algorithms are usually considered in L, the class of problems requiring $O (log n)$ additional space, to be in-place. This class is more in line with the practical definition, as it allows numbers of size $n$ as pointers or indices. This expanded definition still excludes quicksort, however, because of its recursive calls.

Identifying the in-place algorithms with L has some interesting implications; for example, it means that there is a (rather complex) in-place algorithm to determine whether a path exists between two nodes in an undirected graph,^[3] a problem that requires $O (n)$ extra space using typical algorithms such as depth-first search (a visited bit for each node). This in turn yields in-place algorithms for problems such as determining if a graph is bipartite or testing whether two graphs have the same number of connected components.

Role of randomness

In many cases, the space requirements of an algorithm can be drastically cut by using a randomized algorithm. For example, if one wishes to know if two vertices in a graph of $n$ vertices are in the same connected component of the graph, there is no known simple, deterministic, in-place algorithm to determine this. However, if we simply start at one vertex and perform a random walk of about $20 n 3$ steps, the chance that we will stumble across the other vertex provided that it is in the same component is very high. Similarly, there are simple randomized in-place algorithms for primality testing such as the Miller–Rabin primality test, and there are also simple in-place randomized factoring algorithms such as Pollard's rho algorithm.

In functional programming

Functional programming languages often discourage or do not support explicit in-place algorithms that overwrite data, since this is a type of side effect; instead, they only allow new data to be constructed. However, good functional language compilers will often recognize when an object very similar to an existing one is created and then the old one is thrown away, and will optimize this into a simple mutation "under the hood".

Note that it is possible in principle to carefully construct in-place algorithms that do not modify data (unless the data is no longer being used), but this is rarely done in practice.

Related Research Articles

<span class="mw-page-title-main">Heapsort</span> A sorting algorithm which uses the heap data structure

In computer science, heapsort is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly find the largest element in each step.

<span class="mw-page-title-main">Insertion sort</span> Sorting algorithm

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

<span class="mw-page-title-main">Merge sort</span> Divide and conquer-based sorting algorithm

In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.

In computer science, radix sort is a non-comparative sorting algorithm. It avoids comparison by creating and distributing elements into buckets according to their radix. For elements with more than one significant digit, this bucketing process is repeated for each digit, while preserving the ordering of the prior step, until all digits have been considered. For this reason, radix sort has also been called bucket sort and digital sort.

<span class="mw-page-title-main">Sorting algorithm</span> Algorithm that arranges lists in order

In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.

Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, a generalization of pigeonhole sort that allows multiple keys per bucket, and is a cousin of radix sort in the most-to-least significant digit flavor. Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm. The computational complexity depends on the algorithm used to sort each bucket, the number of buckets to use, and whether the input is uniformly distributed.

Introsort or introspective sort is a hybrid sorting algorithm that provides both fast average performance and (asymptotically) optimal worst-case performance. It begins with quicksort, it switches to heapsort when the recursion depth exceeds a level based on (the logarithm of) the number of elements being sorted and it switches to insertion sort when the number of elements is below some threshold. This combines the good parts of the three algorithms, with practical performance comparable to quicksort on typical data sets and worst-case O(n log n) runtime due to the heap sort. Since the three algorithms it uses are comparison sorts, it is also a comparison sort.

In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output are random variables.

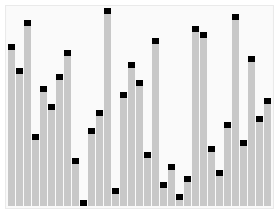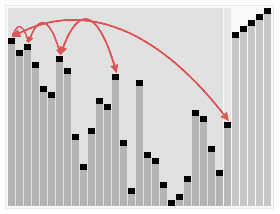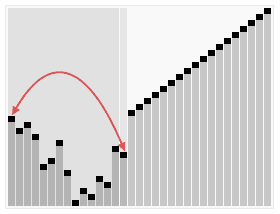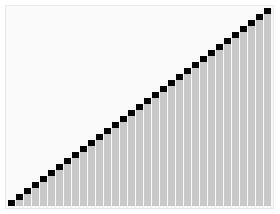
In computer science, patience sorting is a sorting algorithm inspired by, and named after, the card game patience. A variant of the algorithm efficiently computes the length of a longest increasing subsequence in a given array.

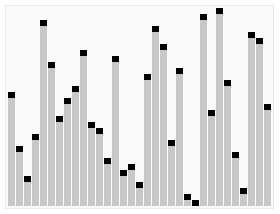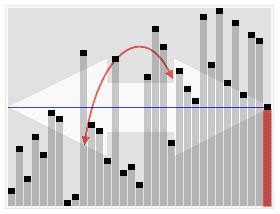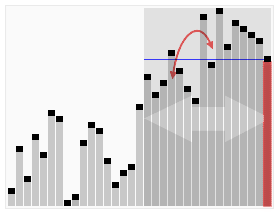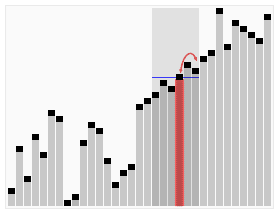
<span class="mw-page-title-main">Quickselect</span> Algorithm for the kth smallest element in an array

In computer science, quickselect is a selection algorithm to find the kth smallest element in an unordered list, also known as the kth order statistic. Like the related quicksort sorting algorithm, it was developed by Tony Hoare, and thus is also known as Hoare's selection algorithm. Like quicksort, it is efficient in practice and has good average-case performance, but has poor worst-case performance. Quickselect and its variants are the selection algorithms most often used in efficient real-world implementations.

<span class="mw-page-title-main">Quicksort</span> Divide and conquer sorting algorithm

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.

sort is a generic function in the C++ Standard Library for doing comparison sorting. The function originated in the Standard Template Library (STL).

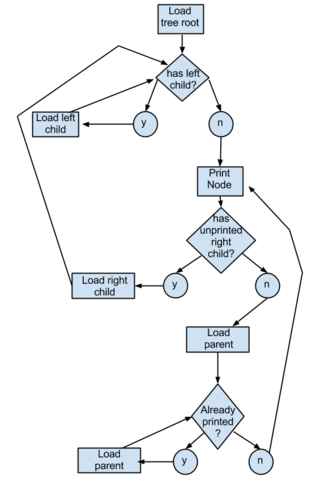
A tree sort is a sort algorithm that builds a binary search tree from the elements to be sorted, and then traverses the tree (in-order) so that the elements come out in sorted order. Its typical use is sorting elements online: after each insertion, the set of elements seen so far is available in sorted order.

Spreadsort is a sorting algorithm invented by Steven J. Ross in 2002. It combines concepts from distribution-based sorts, such as radix sort and bucket sort, with partitioning concepts from comparison sorts such as quicksort and mergesort. In experimental results it was shown to be highly efficient, often outperforming traditional algorithms such as quicksort, particularly on distributions exhibiting structure and string sorting. There is an open-source implementation with performance analysis and benchmarks, and HTML documentation .

Flashsort is a distribution sorting algorithm showing linear computational complexity $O (n)$ for uniformly distributed data sets and relatively little additional memory requirement. The original work was published in 1998 by Karl-Dietrich Neubert.

Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size $s$ from the $n$ -element sequence, and determining the range of the buckets by sorting the sample and choosing $p -1 < s$ elements from the result. These elements then divide the array into $p$ approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.

In computer science, partial sorting is a relaxed variant of the sorting problem. Total sorting is the problem of returning a list of items such that its elements all appear in order, while partial sorting is returning a list of the k smallest elements in order. The other elements may also be sorted, as in an in-place partial sort, or may be discarded, which is common in streaming partial sorts. A common practical example of partial sorting is computing the "Top 100" of some list.

In computer science, k-way merge algorithms or multiway merges are a specific type of sequence merge algorithms that specialize in taking in k sorted lists and merging them into a single sorted list. These merge algorithms generally refer to merge algorithms that take in a number of sorted lists greater than two. Two-way merges are also referred to as binary merges.The k- way merge also external sorting algorithm.

Proportion extend sort is an in-place, comparison-based sorting algorithm which attempts to improve on the performance, particularly the worst-case performance, of quicksort.

References

↑ The bit space requirement of a pointer is $O (log n)$ , but pointer size can be considered a constant in most sorting applications.
↑ Maciej Liśkiewicz and Rüdiger Reischuk. The Complexity World below Logarithmic Space. Structure in Complexity Theory Conference, pp. 64-78. 1994. Online: p. 3, Theorem 2.
↑ Reingold, Omer (2008), "Undirected connectivity in log-space", Journal of the ACM , 55 (4): 1–24, doi:10.1145/1391289.1391291, MR 2445014, S2CID 207168478, ECCC TR04-094

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] The bit space requirement of a pointer is $O (log n)$ , but pointer size can be considered a constant in most sorting applications.

[2] Maciej Liśkiewicz and Rüdiger Reischuk. The Complexity World below Logarithmic Space. Structure in Complexity Theory Conference, pp. 64-78. 1994. Online: p. 3, Theorem 2.

[3] Reingold, Omer (2008), "Undirected connectivity in log-space", Journal of the ACM , 55 (4): 1–24, doi:10.1145/1391289.1391291, MR 2445014, S2CID 207168478, ECCC TR04-094

[1]

[2]

[3]