In commutative algebra, the prime spectrum of a ring R is the set of all prime ideals of R, and is usually denoted by ; in algebraic geometry it is simultaneously a topological space equipped with the sheaf of rings .
The fundamental theorem of algebra, also called d'Alembert's theorem or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.
In mathematics, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of ring properties that are not specific to commutative rings. This distinction results from the high number of fundamental properties of commutative rings that do not extend to noncommutative rings.
In mathematics, Hilbert's Nullstellensatz is a theorem that establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields. This relationship was discovered by David Hilbert, who proved the Nullstellensatz in his second major paper on invariant theory in 1893.
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of n polynomials in n indeterminates. In its original form the theorem states that in general the number of common zeros equals the product of the degrees of the polynomials. It is named after Étienne Bézout.
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The characteristic polynomial of an endomorphism of a finite-dimensional vector space is the characteristic polynomial of the matrix of that endomorphism over any base. The characteristic equation, also known as the determinantal equation, is the equation obtained by equating the characteristic polynomial to zero.

Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
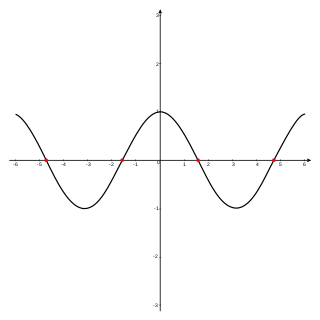
In mathematics, a zero of a real-, complex-, or generally vector-valued function , is a member of the domain of such that vanishes at ; that is, the function attains the value of 0 at , or equivalently, is a solution to the equation . A "zero" of a function is thus an input value that produces an output of 0.

In algebraic geometry, an affine algebraic set is the set of the common zeros over an algebraically closed field k of some family of polynomials in the polynomial ring An affine variety or affine algebraic variety, is an affine algebraic set such that the ideal generated by the defining polynomials is prime.

In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .
In mathematics, a Cohen–Macaulay ring is a commutative ring with some of the algebro-geometric properties of a smooth variety, such as local equidimensionality. Under mild assumptions, a local ring is Cohen–Macaulay exactly when it is a finitely generated free module over a regular local subring. Cohen–Macaulay rings play a central role in commutative algebra: they form a very broad class, and yet they are well understood in many ways.
In commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class that includes finite fields. The endomorphism maps every element to its p-th power. In certain contexts it is an automorphism, but this is not true in general.
In linear algebra, it is often important to know which vectors have their directions unchanged by a linear transformation. An eigenvector or characteristic vector is such a vector. Thus an eigenvector of a linear transformation is scaled by a constant factor when the linear transformation is applied to it: . The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor .
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root, or, equivalently, a common factor. In some older texts, the resultant is also called the eliminant.
In mathematics, intersection theory is one of the main branches of algebraic geometry, where it gives information about the intersection of two subvarieties of a given variety. The theory for varieties is older, with roots in Bézout's theorem on curves and elimination theory. On the other hand, the topological theory more quickly reached a definitive form.
In mathematics, Macdonald polynomialsPλ(x; t,q) are a family of orthogonal symmetric polynomials in several variables, introduced by Macdonald in 1987. He later introduced a non-symmetric generalization in 1995. Macdonald originally associated his polynomials with weights λ of finite root systems and used just one variable t, but later realized that it is more natural to associate them with affine root systems rather than finite root systems, in which case the variable t can be replaced by several different variables t=(t1,...,tk), one for each of the k orbits of roots in the affine root system. The Macdonald polynomials are polynomials in n variables x=(x1,...,xn), where n is the rank of the affine root system. They generalize many other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomials and Askey–Wilson polynomials, which in turn include most of the named 1-variable orthogonal polynomials as special cases. Koornwinder polynomials are Macdonald polynomials of certain non-reduced root systems. They have deep relationships with affine Hecke algebras and Hilbert schemes, which were used to prove several conjectures made by Macdonald about them.
In algebraic geometry, a morphism between algebraic varieties is a function between the varieties that is given locally by polynomials. It is also called a regular map. A morphism from an algebraic variety to the affine line is also called a regular function. A regular map whose inverse is also regular is called biregular, and the biregular maps are the isomorphisms of algebraic varieties. Because regular and biregular are very restrictive conditions – there are no non-constant regular functions on projective varieties – the concepts of rational and birational maps are widely used as well; they are partial functions that are defined locally by rational fractions instead of polynomials.
The concept of a Projective space plays a central role in algebraic geometry. This article aims to define the notion in terms of abstract algebraic geometry and to describe some basic uses of projective spaces.
In algebraic geometry, the main theorem of elimination theory states that every projective scheme is proper. A version of this theorem predates the existence of scheme theory. It can be stated, proved, and applied in the following more classical setting. Let k be a field, denote by the n-dimensional projective space over k. The main theorem of elimination theory is the statement that for any n and any algebraic variety V defined over k, the projection map sends Zariski-closed subsets to Zariski-closed subsets.






















































