
In mathematics, an associative algebraA is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field K. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.

In geometry and physics, spinors are elements of a complex number-based vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation, but unlike geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360°. It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors.

In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry, theoretical physics and digital image processing. They are named after the English mathematician William Kingdon Clifford (1845–1879).
In mathematics, hypercomplex number is a traditional term for an element of a finite-dimensional unital algebra over the field of real numbers. The study of hypercomplex numbers in the late 19th century forms the basis of modern group representation theory.
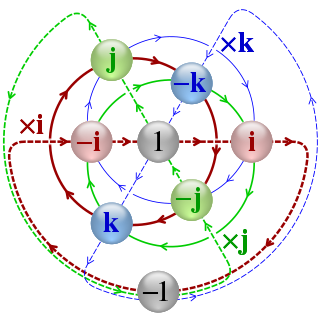
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.

In mathematics, the cross product or vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space, and is denoted by the symbol . Given two linearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. The units of the cross-product are the product of the units of each vector. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.
In mathematics, the tensor algebra of a vector space V, denoted T(V) or T•(V), is the algebra of tensors on V (of any rank) with multiplication being the tensor product. It is the free algebra on V, in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property (see below).

In mathematics the spin group Spin(n) is a Lie group whose underlying manifold is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups (when n ≠ 2)
In abstract algebra, the Weyl algebra is the ring of differential operators with polynomial coefficients, namely expressions of the form
In mathematics, the complexification of a vector space V over the field of real numbers yields a vector space VC over the complex number field, obtained by formally extending the scaling of vectors by real numbers to include their scaling ("multiplication") by complex numbers. Any basis for V may also serve as a basis for VC over the complex numbers.
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by Raoul Bott, which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy groups of spheres. Bott periodicity can be formulated in numerous ways, with the periodicity in question always appearing as a period-2 phenomenon, with respect to dimension, for the theory associated to the unitary group. See for example topological K-theory.
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras for a nondegenerate quadratic form have been completely classified. In each case, the Clifford algebra is algebra isomorphic to a full matrix ring over R, C, or H, or to a direct sum of two copies of such an algebra, though not in a canonical way. Below it is shown that distinct Clifford algebras may be algebra-isomorphic, as is the case of Cl1,1(R) and Cl2,0(R), which are both isomorphic as rings to the ring of two-by-two matrices over the real numbers.
In abstract algebra, the biquaternions are the numbers w + xi + yj + zk, where w, x, y, and z are complex numbers, or variants thereof, and the elements of {1, i, j, k} multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions corresponding to complex numbers and the variations thereof:
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.
In mathematics, a super vector space is a -graded vector space, that is, a vector space over a field with a given decomposition of subspaces of grade and grade . The study of super vector spaces and their generalizations is sometimes called super linear algebra. These objects find their principal application in theoretical physics where they are used to describe the various algebraic aspects of supersymmetry.
In mathematics—more specifically, in differential geometry—the musical isomorphism is an isomorphism between the tangent bundle and the cotangent bundle of a pseudo-Riemannian manifold induced by its metric tensor. There are similar isomorphisms on symplectic manifolds. The term musical refers to the use of the symbols (flat) and (sharp).

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε2 = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.

A gyrovector space is a mathematical concept proposed by Abraham A. Ungar for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. Ungar introduced the concept of gyrovectors that have addition based on gyrogroups instead of vectors which have addition based on groups. Ungar developed his concept as a tool for the formulation of special relativity as an alternative to the use of Lorentz transformations to represent compositions of velocities. This is achieved by introducing "gyro operators"; two 3d velocity vectors are used to construct an operator, which acts on another 3d velocity.
In mathematics, a bivector is the vector part of a biquaternion. For biquaternion q = w + xi + yj + zk, w is called the biscalar and xi + yj + zk is its bivector part. The coordinates w, x, y, z are complex numbers with imaginary unit h:





























