
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.
In differential geometry, a Riemannian manifold or Riemannian space(M, g), so called after the German mathematician Bernhard Riemann, is a real, smooth manifold M equipped with a positive-definite inner product gp on the tangent space TpM at each point p.
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space.
In the mathematical field of Riemannian geometry, the scalar curvature is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geometry of the metric near that point. It is defined by a complicated explicit formula in terms of partial derivatives of the metric components, although it is also characterized by the volume of infinitesimally small geodesic balls. In the context of the differential geometry of surfaces, the scalar curvature is twice the Gaussian curvature, and completely characterizes the curvature of a surface. In higher dimensions, however, the scalar curvature only represents one particular part of the Riemann curvature tensor.
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed.
In mathematics, conformal geometry is the study of the set of angle-preserving (conformal) transformations on a space.
In the mathematical field of differential geometry, Ricci-flatness is a condition on the curvature of a (pseudo-)Riemannian manifold. Ricci-flat manifolds are a special kind of Einstein manifold. In theoretical physics, Ricci-flat Lorentzian manifolds are of fundamental interest, as they are the solutions of Einstein's field equations in vacuum with vanishing cosmological constant.
In geometry, the line element or length element can be informally thought of as a line segment associated with an infinitesimal displacement vector in a metric space. The length of the line element, which may be thought of as a differential arc length, is a function of the metric tensor and is denoted by .

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
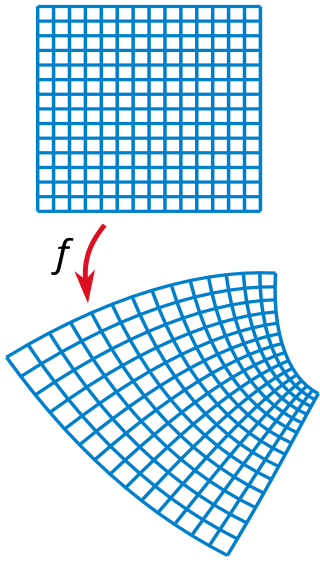
A (pseudo-)Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.
In mathematics, more precisely in differential geometry, a soldering of a fiber bundle to a smooth manifold is a manner of attaching the fibers to the manifold in such a way that they can be regarded as tangent. Intuitively, soldering expresses in abstract terms the idea that a manifold may have a point of contact with a certain model Klein geometry at each point. In extrinsic differential geometry, the soldering is simply expressed by the tangency of the model space to the manifold. In intrinsic geometry, other techniques are needed to express it. Soldering was introduced in this general form by Charles Ehresmann in 1950.
The tetrad formalism is an approach to general relativity that generalizes the choice of basis for the tangent bundle from a coordinate basis to the less restrictive choice of a local basis, i.e. a locally defined set of four linearly independent vector fields called a tetrad or vierbein. It is a special case of the more general idea of a vielbein formalism, which is set in (pseudo-)Riemannian geometry. This article as currently written makes frequent mention of general relativity; however, almost everything it says is equally applicable to (pseudo-)Riemannian manifolds in general, and even to spin manifolds. Most statements hold simply by substituting arbitrary for . In German, "vier" translates to "four", and "viel" to "many".
In differential geometry there are a number of second-order, linear, elliptic differential operators bearing the name Laplacian. This article provides an overview of some of them.
In mathematics and physics, a recurrent tensor, with respect to a connection on a manifold M, is a tensor T for which there is a one-form ω on M such that
Riemannian most often refers to Bernhard Riemann:
In the mathematical field of differential geometry, a Frobenius manifold, introduced by Dubrovin, is a flat Riemannian manifold with a certain compatible multiplicative structure on the tangent space. The concept generalizes the notion of Frobenius algebra to tangent bundles.
John "Jack" Marshall Lee is an American mathematician and professor at the University of Washington specializing in differential geometry.


