
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ; every complex number can be expressed in the form , where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number ,a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world.
In mathematics, an elementary function is a function of a single variable that is defined as taking sums, products, roots and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, and exponential functions, including possibly their inverse functions.
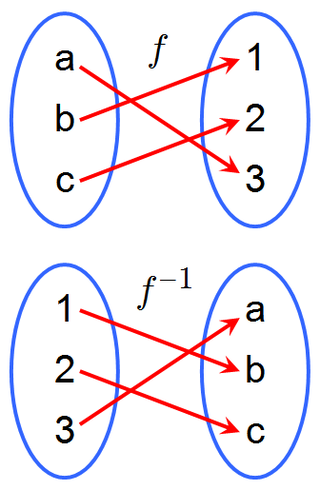
In mathematics, the inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

In mathematics, a square root of a number x is a number y such that ; in other words, a number y whose square is x. For example, 4 and −4 are square roots of 16 because .

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

The imaginary unit or unit imaginary number is a solution to the quadratic equation x2 + 1 = 0. Although there is no real number with this property, i can be used to extend the real numbers to what are called complex numbers, using addition and multiplication. A simple example of the use of i in a complex number is 2 + 3i.

In mathematics, exponentiation is an operation involving two numbers: the base and the exponent or power. Exponentiation is written as bn, where b is the base and n is the power; this is pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
In mathematics, taking the nth root is an operation involving two numbers, the radicand and the index or degree. Taking the nth root is written as , where x is the radicand and n is the index. This is pronounced as "the nth root of x". The definition then of an nth root of a number x is a number r which, when raised to the power of the positive integer n, yields x:

In mathematics, the Gudermannian function relates a hyperbolic angle measure to a circular angle measure called the gudermannian of and denoted . The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude when parameter

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
In mathematics, specifically complex analysis, the principal values of a multivalued function are the values along one chosen branch of that function, so that it is single-valued. A simple case arises in taking the square root of a positive real number. For example, 4 has two square roots: 2 and −2; of these the positive root, 2, is considered the principal root and is denoted as
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that if the function is n-valued at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept.
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.
In mathematics, a principal branch is a function which selects one branch ("slice") of a multi-valued function. Most often, this applies to functions defined on the complex plane.

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among others.

In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangent, inverse hyperbolic cosecant, inverse hyperbolic secant, and inverse hyperbolic cotangent. They are commonly denoted by the symbols for the hyperbolic functions, prefixed with arc- or ar-.

In computing and mathematics, the function atan2 is the 2-argument arctangent. By definition, is the angle measure between the positive -axis and the ray from the origin to the point in the Cartesian plane. Equivalently, is the argument of the complex number

In mathematics, a complex logarithm is a generalization of the natural logarithm to nonzero complex numbers. The term refers to one of the following, which are strongly related:

In mathematics (particularly in complex analysis), the argument of a complex number z, denoted arg(z), is the angle between the positive real axis and the line joining the origin and z, represented as a point in the complex plane, shown as in Figure 1. By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign.
































