The neutron is a subatomic particle, symbol
n
or
n0
, which has a neutral charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons behave similarly within the nucleus, and each has a mass of approximately one dalton, they are both referred to as nucleons. Their properties and interactions are described by nuclear physics. Protons and neutrons are not elementary particles; each is composed of three quarks.

Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.

In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.
In nuclear physics and particle physics, the strong interaction, which is also often called the strong force or strong nuclear force, is a fundamental interaction that confines quarks into protons, neutrons, and other hadron particles. The strong interaction also binds neutrons and protons to create atomic nuclei, where it is called the nuclear force.

In nuclear physics, atomic physics, and nuclear chemistry, the nuclear shell model utilizes the Pauli exclusion principle in order to model the structure of atomic nuclei in terms of energy levels. The first shell model was proposed by Dmitri Ivanenko in 1932. The model was developed in 1949 following independent work by several physicists, most notably Maria Goeppert Mayer and J. Hans D. Jensen, who shared half of the 1963 Nobel Prize in Physics for their contributions.
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.

In quantum physics and chemistry, quantum numbers describe values of conserved quantities in the dynamics of a quantum system. Quantum numbers correspond to eigenvalues of operators that commute with the Hamiltonian—quantities that can be known with precision at the same time as the system's energy—and their corresponding eigenspaces. Together, a specification of all of the quantum numbers of a quantum system fully characterize a basis state of the system, and can in principle be measured together.

In nuclear physics, a magic number is a number of nucleons such that they are arranged into complete shells within the atomic nucleus. As a result, atomic nuclei with a 'magic' number of protons or neutrons are much more stable than other nuclei. The seven most widely recognized magic numbers as of 2019 are 2, 8, 20, 28, 50, 82, and 126.

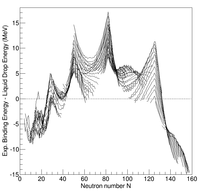
In nuclear physics, the semi-empirical mass formula (SEMF) is used to approximate the mass of an atomic nucleus from its number of protons and neutrons. As the name suggests, it is based partly on theory and partly on empirical measurements. The formula represents the liquid-drop model proposed by George Gamow, which can account for most of the terms in the formula and gives rough estimates for the values of the coefficients. It was first formulated in 1935 by German physicist Carl Friedrich von Weizsäcker, and although refinements have been made to the coefficients over the years, the structure of the formula remains the same today.
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
In quantum mechanics, angular momentum coupling is the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta. For instance, the orbit and spin of a single particle can interact through spin–orbit interaction, in which case the complete physical picture must include spin–orbit coupling. Or two charged particles, each with a well-defined angular momentum, may interact by Coulomb forces, in which case coupling of the two one-particle angular momenta to a total angular momentum is a useful step in the solution of the two-particle Schrödinger equation. In both cases the separate angular momenta are no longer constants of motion, but the sum of the two angular momenta usually still is. Angular momentum coupling in atoms is of importance in atomic spectroscopy. Angular momentum coupling of electron spins is of importance in quantum chemistry. Also in the nuclear shell model angular momentum coupling is ubiquitous.

The nuclear force is a force that acts between hadrons, most commonly observed between protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nuclear force almost identically. Since protons have charge +1 e, they experience an electric force that tends to push them apart, but at short range the attractive nuclear force is strong enough to overcome the electrostatic force. The nuclear force binds nucleons into atomic nuclei.

Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons. The binding energy for stable nuclei is always a positive number, as the nucleus must gain energy for the nucleons to move apart from each other. Nucleons are attracted to each other by the strong nuclear force. In theoretical nuclear physics, the nuclear binding energy is considered a negative number. In this context it represents the energy of the nucleus relative to the energy of the constituent nucleons when they are infinitely far apart. Both the experimental and theoretical views are equivalent, with slightly different emphasis on what the binding energy means.

In nuclear physics, the valley of stability is a characterization of the stability of nuclides to radioactivity based on their binding energy. Nuclides are composed of protons and neutrons. The shape of the valley refers to the profile of binding energy as a function of the numbers of neutrons and protons, with the lowest part of the valley corresponding to the region of most stable nuclei. The line of stable nuclides down the center of the valley of stability is known as the line of beta stability. The sides of the valley correspond to increasing instability to beta decay. The decay of a nuclide becomes more energetically favorable the further it is from the line of beta stability. The boundaries of the valley correspond to the nuclear drip lines, where nuclides become so unstable they emit single protons or single neutrons. Regions of instability within the valley at high atomic number also include radioactive decay by alpha radiation or spontaneous fission. The shape of the valley is roughly an elongated paraboloid corresponding to the nuclide binding energies as a function of neutron and atomic numbers.

The Woods–Saxon potential is a mean field potential for the nucleons inside the atomic nucleus, which is used to describe approximately the forces applied on each nucleon, in the nuclear shell model for the structure of the nucleus. The potential is named after Roger D. Woods and David S. Saxon.

The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford based on the 1909 Geiger–Marsden gold foil experiment. After the discovery of the neutron in 1932, models for a nucleus composed of protons and neutrons were quickly developed by Dmitri Ivanenko and Werner Heisenberg. An atom is composed of a positively charged nucleus, with a cloud of negatively charged electrons surrounding it, bound together by electrostatic force. Almost all of the mass of an atom is located in the nucleus, with a very small contribution from the electron cloud. Protons and neutrons are bound together to form a nucleus by the nuclear force.

The nuclear drip line is the boundary beyond which atomic nuclei are unbound with respect to the emission of a proton or neutron.

In nuclear physics, ab initio methods seek to describe the atomic nucleus from the bottom up by solving the non-relativistic Schrödinger equation for all constituent nucleons and the forces between them. This is done either exactly for very light nuclei or by employing certain well-controlled approximations for heavier nuclei. Ab initio methods constitute a more fundamental approach compared to e.g. the nuclear shell model. Recent progress has enabled ab initio treatment of heavier nuclei such as nickel.
The Nilsson model is a nuclear shell model treating the atomic nucleus as a deformed sphere. In 1953, the first experimental examples were found of rotational bands in nuclei, with their energy levels following the same J(J+1) pattern of energies as in rotating molecules. Quantum mechanically, it is impossible to have a collective rotation of a sphere, so this implied that the shape of these nuclei was nonspherical. In principle, these rotational states could have been described as coherent superpositions of particle-hole excitations in the basis consisting of single-particle states of the spherical potential. But in reality, the description of these states in this manner is intractable, due to the large number of valence particles—and this intractability was even greater in the 1950s, when computing power was extremely rudimentary. For these reasons, Aage Bohr, Ben Mottelson, and Sven Gösta Nilsson constructed models in which the potential was deformed into an ellipsoidal shape. The first successful model of this type is the one now known as the Nilsson model. It is essentially a nuclear shell model using a harmonic oscillator potential, but with anisotropy added, so that the oscillator frequencies along the three Cartesian axes are not all the same. Typically the shape is a prolate ellipsoid, with the axis of symmetry taken to be z.