
A Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.

In Euclidean geometry, an affine transformation, or an affinity, is a geometric transformation that preserves lines and parallelism.

In geometry, the stereographic projection is a particular mapping (function) that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point: the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it preserves angles at which curves meet. It is neither isometric nor area-preserving: that is, it preserves neither distances nor the areas of figures.
In mathematics, a quadric or quadric surface, is a generalization of conic sections. It is a hypersurface in a (D + 1)-dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in D + 1 variables. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a degenerate quadric or a reducible quadric.

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.

A Projection is a design technique used to display a n-dimensional object on a n − 1 dimensional surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. This concept of extending 2D geometry to 3D was mastered by Heron of Alexandria in the first century. Heron could be called the father of 3D. 3D Projection is the basis of the concept for Computer Graphics simulating fluid flows to imitate realistic effects. Lucas Films 'ILM group is credited with introducing the concept.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have sign : a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

Oblique projection is a simple type of technical drawing of graphical projection used for producing two-dimensional (2D) images of three-dimensional (3D) objects.

In linear algebra and functional analysis, a projection is a linear transformation from a vector space to itself such that . That is, whenever is applied twice to any vector, it gives the same result as if it were applied once. It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.
A zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorov, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope.
In linear algebra, linear transformations can be represented by matrices. If is a linear transformation mapping to and is a column vector with entries, then

In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.
In mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation. In algebraic geometry, the twisted cubic is a simple example of a projective variety that is not linear or a hypersurface, in fact not a complete intersection. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line.

In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion.
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation.

Three-dimensional space is a geometric setting in which three values are required to determine the position of an element. This is the informal meaning of the term dimension.

The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection.
In mathematics, a projection is a mapping of a set into a subset, which is equal to its square for mapping composition, i.e., which is idempotent. The restriction to a subspace of a projection is also called a projection, even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane : the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a closed disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are:
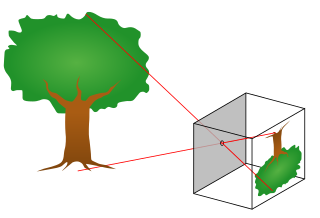
The pinhole camera model describes the mathematical relationship between the coordinates of a point in three-dimensional space and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light. The model does not include, for example, geometric distortions or blurring of unfocused objects caused by lenses and finite sized apertures. It also does not take into account that most practical cameras have only discrete image coordinates. This means that the pinhole camera model can only be used as a first order approximation of the mapping from a 3D scene to a 2D image. Its validity depends on the quality of the camera and, in general, decreases from the center of the image to the edges as lens distortion effects increase.
















