Strict 2-category

Last updated June 06, 2023

In category theory, a strict 2-category is a category with "morphisms between morphisms", that is, where each hom-set itself carries the structure of a category. It can be formally defined as a category enriched over Cat (the category of categories and functors, with the monoidal structure given by product of categories).

Definition

A 2-category C consists of:

A class of 0-cells (or objects ) $A$ , $B$ , ....
For all objects $A$ and $B$ , a category $\mathbf {C} (A,B)$ . The objects $f,g:A\to B$ of this category are called 1-cells and its morphisms $\alpha :f\Rightarrow g$ are called 2-cells; the composition in this category is usually written $\circ$ or $\circ _{1}$ and called vertical composition or composition along a 1-cell.
For any object $A$ there is a functor from the terminal category (with one object and one arrow) to $\mathbf {C} (A,A)$ that picks out the identity 1-cell $id A$ on $A$ and its identity 2-cell $id id A$ . In practice these two are often denoted simply by $A$ .
For all objects $A$ , $B$ and $C$ , there is a functor $\circ _{0}\colon \mathbf {C} (B,C)\times \mathbf {C} (A,B)\to \mathbf {C} (A,C)$ , called horizontal composition or composition along a 0-cell, which is associative and admits^{[ clarification needed ]} the identity 1 and 2-cells of $id A$ as identities. Here, associativity for $\circ _{0}$ means that horizontally composing $\mathbf {C} (C,D)\times \mathbf {C} (B,C)\times \mathbf {C} (A,B)$ twice to $\mathbf {C} (A,D)$ is independent of which of the two $\mathbf {C} (C,D)\times \mathbf {C} (B,C)$ and $\mathbf {C} (B,C)\times \mathbf {C} (A,B)$ are composed first. The composition symbol $\circ _{0}$ is often omitted, the horizontal composite of 2-cells $\alpha \colon f\Rightarrow g\colon A\to B$ and $\beta \colon f'\Rightarrow g'\colon B\to C$ being written simply as $\beta \alpha \colon f'f\Rightarrow g'g\colon A\to C$ .

The 0-cells, 1-cells, and 2-cells terminology is replaced by 0-morphisms, 1-morphisms, and 2-morphisms in some sources^[3] (see also Higher category theory).

The notion of 2-category differs from the more general notion of a bicategory in that composition of 1-cells (horizontal composition) is required to be strictly associative, whereas in a bicategory it needs only be associative up to a 2-isomorphism. The axioms of a 2-category are consequences of their definition as Cat-enriched categories:

Vertical composition is associative and unital, the units being the identity 2-cells $id f$ .
Horizontal composition is also (strictly) associative and unital, the units being the identity 2-cells $id id A$ on the identity 1-cells $id A$ .
The interchange law holds; i.e. it is true that for composable 2-cells $\alpha ,\beta ,\gamma ,\delta$

(\alpha \circ _{0}\beta )\circ _{1}(\gamma \circ _{0}\delta )=(\alpha \circ _{1}\gamma )\circ _{0}(\beta \circ _{1}\delta )

The interchange law follows from the fact that $\circ _{0}$ is a functor between hom categories. It can be drawn as a pasting diagram as follows:

	=	=	$\circ _{0}$
$\circ _{1}$

Here the left-hand diagram denotes the vertical composition of horizontal composites, the right-hand diagram denotes the horizontal composition of vertical composites, and the diagram in the centre is the customary representation of both. The 2-cell are drawn with double arrows ⇒, the 1-cell with single arrows →, and the 0-cell with points.

Examples

The category Ord (of preordered sets) is a 2-category since preordered sets can easily be interpreted as categories.

Category of small categories

The archetypal 2-category is the category of small categories, with natural transformations serving as 2-morphisms; typically 2-morphisms are given by Greek letters (such as $\alpha$ above) for this reason.

The objects (0-cells) are all small categories, and for all objects $A$ and $B$ the category $\mathbf {C} (A,B)$ is a functor category. In this context, vertical composition is^[4] the composition of natural transformations.

Doctrines

In mathematics, a doctrine is simply a 2-category which is heuristically regarded as a system of theories. For example, algebraic theories, as invented by William Lawvere, is an example of a doctrine, as are multi-sorted theories, operads, categories, and toposes.

The objects of the 2-category are called theories, the 1-morphisms $f\colon A\rightarrow B$ are called models of the $A$ in $B$ , and the 2-morphisms are called morphisms between models.

The distinction between a 2-category and a doctrine is really only heuristic: one does not typically consider a 2-category to be populated by theories as objects and models as morphisms. It is this vocabulary that makes the theory of doctrines worth while.

For example, the 2-category Cat of categories, functors, and natural transformations is a doctrine. One sees immediately that all presheaf categories are categories of models.

As another example, one may take the subcategory of Cat consisting only of categories with finite products as objects and product-preserving functors as 1-morphisms. This is the doctrine of multi-sorted algebraic theories. If one only wanted 1-sorted algebraic theories, one would restrict the objects to only those categories that are generated under products by a single object.

Doctrines were discovered by Jonathan Mock Beck.

Related Research Articles

In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.

In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:

In mathematics, the Yoneda lemma is arguably the most important result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.

In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.

In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g₁, g₂: Y → Z,

In mathematics, specifically in category theory, an additive category is a preadditive category C admitting all finitary biproducts.

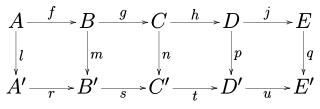
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.

In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint.

In mathematics, a monoidal category is a category $equipped with a bifunctor$

In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.

In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not (strictly) associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.

In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere, although the technique did not become generally known until many years later. Several mathematical concepts can be treated as comma categories. Comma categories also guarantee the existence of some limits and colimits. The name comes from the notation originally used by Lawvere, which involved the comma punctuation mark. The name persists even though standard notation has changed, since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category".

In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms $f : X \to Z$ and $g : Y \to Z$ with a common codomain. The pullback is often written

In mathematics, the derived categoryD(A) of an abelian category A is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on A. The construction proceeds on the basis that the objects of D(A) should be chain complexes in A, with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequences.

In mathematics, specifically in category theory, an $-coalgebra$ is a structure defined according to a functor $, with specific properties as defined below. For both algebras and coalgebras, a functor is a convenient and general way of organizing a signature. This has applications in computer science: examples of coalgebras include lazy, infinite data structures, such as streams, and also transition systems.$

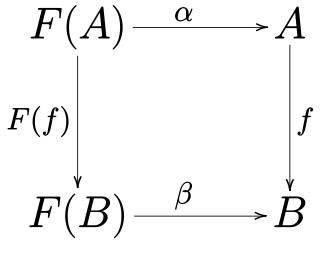
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.

This is a glossary of properties and concepts in category theory in mathematics.

String diagrams are a formal graphical language for representing morphisms in monoidal categories, or more generally 2-cells in 2-categories. They are a prominent tool in applied category theory. When interpreted in the monoidal category of vector spaces and linear maps with the tensor product, string diagrams are called tensor networks or Penrose graphical notation. This has led to the development of categorical quantum mechanics where the axioms of quantum theory are expressed in the language of monoidal categories.

In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors

In category theory, a branch of mathematics, profunctors are a generalization of relations and also of bimodules.

References

↑ Charles Ehresmann, Catégories et structures, Dunod, Paris 1965.
↑ Jean Bénabou, Introduction to bicategories, in Reports of the Midwest Category Seminar, Springer, Berlin, 1967, pp. 1--77.
↑ "2-category in nLab". ncatlab.org. Retrieved 2023-02-20.
↑ "vertical composition in nLab". ncatlab.org. Retrieved 2023-02-20.

Footnotes

Generalised algebraic models, by Claudia Centazzo.

External links

Media related to Strict 2-category at Wikimedia Commons

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Charles Ehresmann, Catégories et structures, Dunod, Paris 1965.

[2] Jean Bénabou, Introduction to bicategories, in Reports of the Midwest Category Seminar, Springer, Berlin, 1967, pp. 1--77.

[3] "2-category in nLab". ncatlab.org. Retrieved 2023-02-20.

[4] "vertical composition in nLab". ncatlab.org. Retrieved 2023-02-20.

[1]

[2]

[3]

[4]