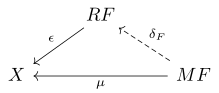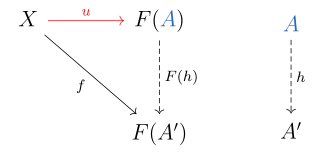
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In mathematics, the Yoneda lemma is arguably the most important result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In mathematics, a self-adjoint operator on an infinite-dimensional complex vector space V with inner product is a linear map A that is its own adjoint. If V is finite-dimensional with a given orthonormal basis, this is equivalent to the condition that the matrix of A is a Hermitian matrix, i.e., equal to its conjugate transpose A∗. By the finite-dimensional spectral theorem, V has an orthonormal basis such that the matrix of A relative to this basis is a diagonal matrix with entries in the real numbers. This article deals with applying generalizations of this concept to operators on Hilbert spaces of arbitrary dimension.
In mathematics, a monoidal category is a category equipped with a bifunctor
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set A can be thought of as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure. Examples include free groups, tensor algebras, or free lattices.
In category theory, a branch of mathematics, a monad is a monoid in the category of endofunctors of some fixed category. An endofunctor is a functor mapping a category to itself, and a monad is an endofunctor together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories. Monads are also useful in the theory of datatypes, the denotational semantics of imperative programming languages, and in functional programming languages, allowing languages with non-mutable states to do things such as simulate for-loops; see Monad.
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
In mathematics, especially in category theory, a closed monoidal category is a category that is both a monoidal category and a closed category in such a way that the structures are compatible.
In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
String diagrams are a formal graphical language for representing morphisms in monoidal categories, or more generally 2-cells in 2-categories. They are a prominent tool in applied category theory. When interpreted in the monoidal category of vector spaces and linear maps with the tensor product, string diagrams are called tensor networks or Penrose graphical notation. This has led to the development of categorical quantum mechanics where the axioms of quantum theory are expressed in the language of monoidal categories.
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
In category theory, a branch of mathematics, profunctors are a generalization of relations and also of bimodules.
In category theory, a branch of mathematics, a presheaf on a category is a functor . If is the poset of open sets in a topological space, interpreted as a category, then one recovers the usual notion of presheaf on a topological space.
In mathematics, Grothendieck's six operations, named after Alexander Grothendieck, is a formalism in homological algebra, also known as the six-functor formalism. It originally sprang from the relations in étale cohomology that arise from a morphism of schemes f : X → Y. The basic insight was that many of the elementary facts relating cohomology on X and Y were formal consequences of a small number of axioms. These axioms hold in many cases completely unrelated to the original context, and therefore the formal consequences also hold. The six operations formalism has since been shown to apply to contexts such as D-modules on algebraic varieties, sheaves on locally compact topological spaces, and motives.
In mathematics, the automorphism group of an object X is the group consisting of automorphisms of X under composition of morphisms. For example, if X is a finite-dimensional vector space, then the automorphism group of X is the group of invertible linear transformations from X to itself. If instead X is a group, then its automorphism group is the group consisting of all group automorphisms of X.
In mathematics, especially in category theory, the codensity monad is a fundamental construction associating a monad to a wide class of functors.