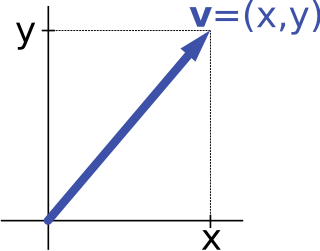In mathematics, a 3-sphere, glome or hypersphere is a higher-dimensional analogue of a sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. Topologically, a 3-sphere is an example of a 3-manifold, and it is also an n-sphere.

In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by H, or in blackboard bold by Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form
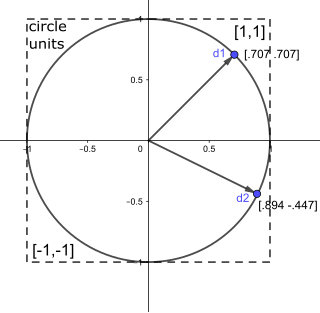
In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in .
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

In mathematics, the special unitary group of degree n, denoted SU(n), is the Lie group of n × n unitary matrices with determinant 1.
Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.
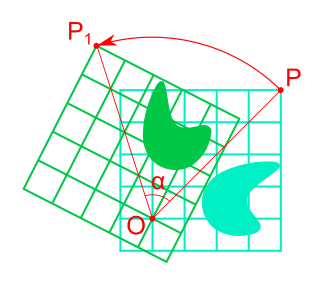
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped from a distinct great circle of the 3-sphere. Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. Considering a scalar as a degree-zero quantity and a vector as a degree-one quantity, a bivector is of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex numbers in two dimensions and to both pseudovectors and vector quaternions in three dimensions. They can be used to generate rotations in a space of any number of dimensions, and are a useful tool for classifying such rotations. They are also used in physics.
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form
In abstract algebra, the biquaternions are the numbers w + xi + yj + zk, where w, x, y, and z are complex numbers, or variants thereof, and the elements of {1, i, j, k} multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions corresponding to complex numbers and the variations thereof:
Screw theory is the algebraic calculation of pairs of vectors, such as angular and linear velocity, or forces and moments, that arise in the kinematics and dynamics of rigid bodies.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
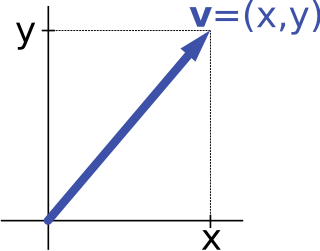
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.

In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector e indicating the direction (geometry) of an axis of rotation, and an angle of rotation θ describing the magnitude and sense of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector e rooted at the origin because the magnitude of e is constrained. For example, the elevation and azimuth angles of e suffice to locate it in any particular Cartesian coordinate frame.
William Rowan Hamilton invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties. Mathematically, quaternions discussed differ from the modern definition only by the terminology which is used.
Six-dimensional space is any space that has six dimensions, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the environment. Of particular interest is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also studied, with constant positive and negative curvature.