Related Research Articles
10 (ten) is the even natural number following 9 and preceding 11. Ten is the base of the decimal numeral system, the most common system of denoting numbers in both spoken and written language.
15 (fifteen) is the natural number following 14 and preceding 16.
21 (twenty-one) is the natural number following 20 and preceding 22.
33 (thirty-three) is the natural number following 32 and preceding 34.
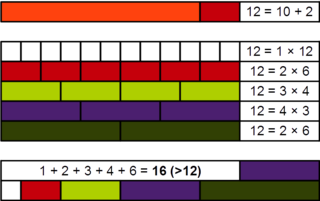
In number theory, an abundant number or excessive number is a positive integer for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.
220 is the natural number following 219 and preceding 221.
1000 or one thousand is the natural number following 999 and preceding 1001. In most English-speaking countries, it can be written with or without a comma or sometimes a period separating the thousands digit: 1,000.
300 is the natural number following 299 and preceding 301.

360 is the natural number following 359 and preceding 361.
144 is the natural number following 143 and preceding 145.
720 is the natural number following 719 and preceding 721.
100,000 (one hundred thousand) is the natural number following 99,999 and preceding 100,001. In scientific notation, it is written as 105.
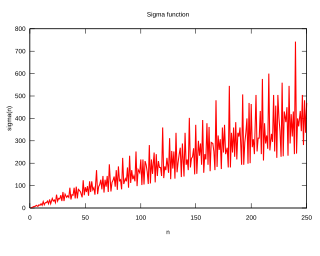
In number theory, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it is defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.
225 is the natural number following 224 and preceding 226.
100,000,000 is the natural number following 99,999,999 and preceding 100,000,001.
168 is the natural number following 167 and preceding 169.
232 is the natural number following 231 and preceding 233.
288 is the natural number following 287 and preceding 289. Because 288 = 2 · 12 · 12, it may also be called "two gross" or "two dozen dozen".
744 is the natural number following 743 and preceding 745.
888 is the natural number following 887 and preceding 889.
References
- ↑ Sloane, N. J. A. (ed.). "SequenceA002182(Highly composite numbers, definition (1): where d(n), the number of divisors of n (A000005), increases to a record)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "SequenceA004394(Superabundant [or super-abundant] numbers: n such that sigma(n)/n > sigma(m)/m for all m<n, sigma(n) being the sum of the divisors of n)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "SequenceA000926(Euler's "numerus idoneus" (or "numeri idonei", or idoneal, or suitable, or convenient numbers))". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "SequenceA003418(Least common multiple (or LCM) of {1, 2, ..., n} for n >= 1)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "SequenceA303704(Numbers k such that all coprime quadratic residues modulo k are squares.)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.