In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.

In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
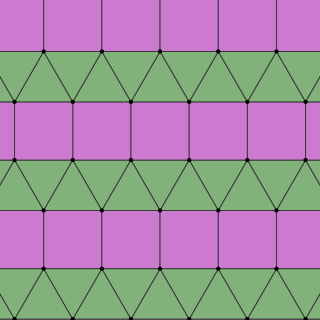
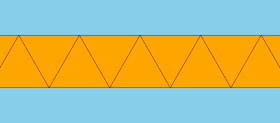
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.
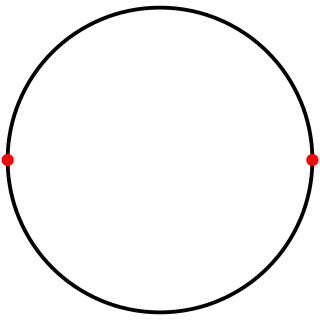
In geometry, a digon is a polygon with two sides (edges) and two vertices. Its construction is degenerate in a Euclidean plane because either the two sides would coincide or one or both would have to be curved; however, it can be easily visualised in elliptic space.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.

In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane.

In geometry, an order-2 apeirogonal tiling, apeirogonal dihedron, or infinite dihedron is a tiling of the plane consisting of two apeirogons. It may be considered an improper regular tiling of the Euclidean plane, with Schläfli symbol {∞, 2}. Two apeirogons, joined along all their edges, can completely fill the entire plane as an apeirogon is infinite in size and has an interior angle of 180°, which is half of a full 360°.

In geometry, the order-3 apeirogonal tiling is a regular tiling of the hyperbolic plane. It is represented by the Schläfli symbol {∞,3}, having three regular apeirogons around each vertex. Each apeirogon is inscribed in a horocycle.

In geometry, the order-4 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,4}.

In the field of hyperbolic geometry, the hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere, a surface in hyperbolic space that approaches a single ideal point at infinity.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere, a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In the field of hyperbolic geometry, the order-6 hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells with an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

The triangular tiling honeycomb is one of 11 paracompact regular space-filling tessellations in hyperbolic 3-space. It is called paracompact because it has infinite cells and vertex figures, with all vertices as ideal points at infinity. It has Schläfli symbol {3,6,3}, being composed of triangular tiling cells. Each edge of the honeycomb is surrounded by three cells, and each vertex is ideal with infinitely many cells meeting there. Its vertex figure is a hexagonal tiling.

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.

In the geometry of hyperbolic 3-space, the order-4 square tiling honeycomb is one of 11 paracompact regular honeycombs. It is paracompact because it has infinite cells and vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {4,4,4}, it has four square tilings around each edge, and infinite square tilings around each vertex in a square tiling vertex figure.

In geometry, an apeirogonal hosohedron or infinite hosohedron is a tiling of the plane consisting of two vertices at infinity. It may be considered an improper regular tiling of the Euclidean plane, with Schläfli symbol {2,∞}.