In geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominoes, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.
For some classes of tilings on a regular grid in two dimensions, it is possible to define a height function associating an integer to the vertices of the grid. For instance, draw a chessboard, fix a node with height 0, then for any node there is a path from to it. On this path define the height of each node (i.e. corners of the squares) to be the height of the previous node plus one if the square on the right of the path from to is black, and minus one otherwise.
More details can be found in Kenyon & Okounkov (2005).
WilliamThurston ( 1990 ) describes a test for determining whether a simply-connected region, formed as the union of unit squares in the plane, has a domino tiling. He forms an undirected graph that has as its vertices the points (x,y,z) in the three-dimensional integer lattice, where each such point is connected to four neighbors: if x + y is even, then (x,y,z) is connected to (x + 1,y,z + 1), (x − 1,y,z + 1), (x,y + 1,z − 1), and (x,y − 1,z − 1), while if x + y is odd, then (x,y,z) is connected to (x + 1,y,z − 1), (x − 1,y,z − 1), (x,y + 1,z + 1), and (x,y − 1,z + 1). The boundary of the region, viewed as a sequence of integer points in the (x,y) plane, lifts uniquely (once a starting height is chosen) to a path in this three-dimensional graph. A necessary condition for this region to be tileable is that this path must close up to form a simple closed curve in three dimensions, however, this condition is not sufficient. Using more careful analysis of the boundary path, Thurston gave a criterion for tileability of a region that was sufficient as well as necessary.
The number of ways to cover an rectangle with dominoes, calculated independently by Temperley & Fisher (1961) and Kasteleyn (1961), is given by
(sequence A099390 in the OEIS)
When both m and n are odd, the formula correctly reduces to zero possible domino tilings.
A special case occurs when tiling the rectangle with n dominoes: the sequence reduces to the Fibonacci sequence. [1]
Another special case happens for squares with m = n = 0, 2, 4, 6, 8, 10, 12, ... is
These numbers can be found by writing them as the Pfaffian of an skew-symmetric matrix whose eigenvalues can be found explicitly. This technique may be applied in many mathematics-related subjects, for example, in the classical, 2-dimensional computation of the dimer-dimer correlator function in statistical mechanics.
The number of tilings of a region is very sensitive to boundary conditions, and can change dramatically with apparently insignificant changes in the shape of the region. This is illustrated by the number of tilings of an Aztec diamond of order n, where the number of tilings is 2(n + 1)n/2. If this is replaced by the "augmented Aztec diamond" of order n with 3 long rows in the middle rather than 2, the number of tilings drops to the much smaller number D(n,n), a Delannoy number, which has only exponential rather than super-exponential growth in n. For the "reduced Aztec diamond" of order n with only one long middle row, there is only one tiling.
Tatami are Japanese floor mats in the shape of a domino (1x2 rectangle). They are used to tile rooms, but with additional rules about how they may be placed. In particular, typically, junctions where three tatami meet are considered auspicious, while junctions where four meet are inauspicious, so a proper tatami tiling is one where only three tatami meet at any corner. [2] The problem of tiling an irregular room by tatami that meet three to a corner is NP-complete. [3]
There is a one-to-one correspondence between a periodic domino tiling and a ground state configuration of the fully-frustrated Ising model on a two-dimensional periodic lattice. [4] To see that, we note that at the ground state, each plaquette of the spin model must contain exactly one frustrated interaction. Therefore, viewing from the dual lattice, each frustrated edge must be "covered" by a 1x2 rectangle, such that the rectangles span the entire lattice and do not overlap, or a domino tiling of the dual lattice.
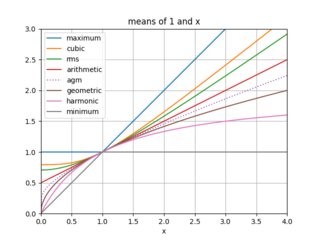
In mathematics, the arithmetic–geometric mean of two positive real numbers x and y is the mutual limit of a sequence of arithmetic means and a sequence of geometric means. The arithmetic–geometric mean is used in fast algorithms for exponential, trigonometric functions, and other special functions, as well as some mathematical constants, in particular, computing π.
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a product.
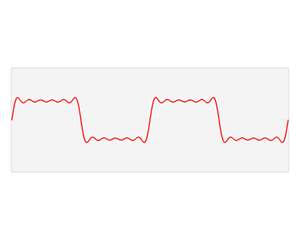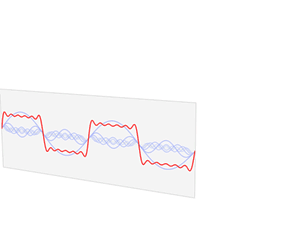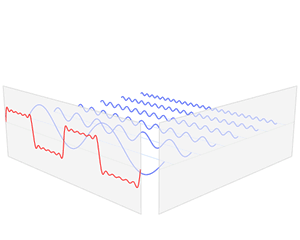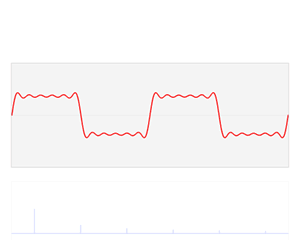
A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.
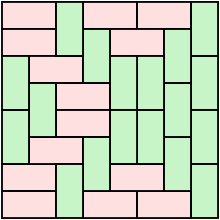
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
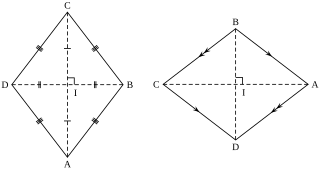
In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in -dimensional Euclidean space.
Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems. The dragon curve is probably most commonly thought of as the shape that is generated from repeatedly folding a strip of paper in half, although there are other curves that are called dragon curves that are generated differently.
In mathematics, physics and engineering, the sinc function, denoted by sinc(x), has two forms, normalized and unnormalized.
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
In mathematics, the plastic ratio is a geometrical proportion close to 53/40. Its true value is the real solution of the equation x3 = x + 1.
The square root of 5 is the positive real number that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio. It can be denoted in surd form as:
In mathematics, the Schröder number also called a large Schröder number or big Schröder number, describes the number of lattice paths from the southwest corner of an grid to the northeast corner using only single steps north, northeast, or east, that do not rise above the SW–NE diagonal.
In mathematics, the Gauss circle problem is the problem of determining how many integer lattice points there are in a circle centered at the origin and with radius . This number is approximated by the area of the circle, so the real problem is to accurately bound the error term describing how the number of points differs from the area. The first progress on a solution was made by Carl Friedrich Gauss, hence its name.
In combinatorial mathematics, an Aztec diamond of order n consists of all squares of a square lattice whose centers (x,y) satisfy |x| + |y| ≤ n. Here n is a fixed integer, and the square lattice consists of unit squares with the origin as a vertex of 4 of them, so that both x and y are half-integers.
In mathematics, a domino is a polyomino of order 2, that is, a polygon in the plane made of two equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there is only one free domino.
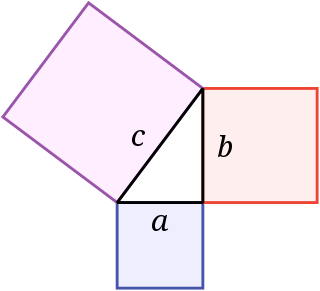
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
