
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger connected, so-called spanning cluster. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles network theory and percolation.

A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as

Network theory is the study of graphs as a representation of either symmetric relations or asymmetric relations between discrete objects. In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes.
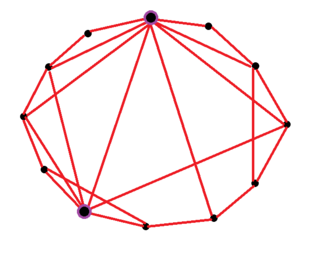
A small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but the neighbors of any given node are likely to be neighbors of each other and most nodes can be reached from every other node by a small number of hops or steps. Specifically, a small-world network is defined to be a network where the typical distance L between two randomly chosen nodes grows proportionally to the logarithm of the number of nodes N in the network, that is:
In graph theory, a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties; this likelihood tends to be greater than the average probability of a tie randomly established between two nodes.

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.
In network theory, a giant component is a connected component of a given random graph that contains a finite fraction of the entire graph's vertices.

The Barabási–Albert (BA) model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Several natural and human-made systems, including the Internet, the world wide web, citation networks, and some social networks are thought to be approximately scale-free and certainly contain few nodes with unusually high degree as compared to the other nodes of the network. The BA model tries to explain the existence of such nodes in real networks. The algorithm is named for its inventors Albert-László Barabási and Réka Albert and is a special case of an earlier and more general model called Price's model.

In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to.
In complex network theory, the fitness model is a model of the evolution of a network: how the links between nodes change over time depends on the fitness of nodes. Fitter nodes attract more links at the expense of less fit nodes.

In the mathematical field of graph theory, the Erdős–Rényi model is either of two closely related models for generating random graphs or the evolution of a random network. They are named after Hungarian mathematicians Paul Erdős and Alfréd Rényi, who first introduced one of the models in 1959, while Edgar Gilbert introduced the other model contemporaneously and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely; in the model introduced by Gilbert, also called the Erdős–Rényi–Gilbert model, each edge has a fixed probability of being present or absent, independently of the other edges. These models can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.
The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability p, or more generally a critical surface for a group of parameters p1, p2, ..., such that infinite connectivity (percolation) first occurs.

Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by nodes and the connections between the elements or actors as links. The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena."

Modularity is a measure of the structure of networks or graphs which measures the strength of division of a network into modules. Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. Modularity is often used in optimization methods for detecting community structure in networks. However, it has been shown that modularity suffers a resolution limit and, therefore, it is unable to detect small communities. Biological networks, including animal brains, exhibit a high degree of modularity.
The clique percolation method is a popular approach for analyzing the overlapping community structure of networks. The term network community has no widely accepted unique definition and it is usually defined as a group of nodes that are more densely connected to each other than to other nodes in the network. There are numerous alternative methods for detecting communities in networks, for example, the Girvan–Newman algorithm, hierarchical clustering and modularity maximization.
In the context of the physical and mathematical theory of percolation, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected to not depend on microscopic details such as the lattice structure, or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.

Hierarchical network models are iterative algorithms for creating networks which are able to reproduce the unique properties of the scale-free topology and the high clustering of the nodes at the same time. These characteristics are widely observed in nature, from biology to language to some social networks.

The study of interdependent networks is a subfield of network science dealing with phenomena caused by the interactions between complex networks. Though there may be a wide variety of interactions between networks, dependency focuses on the scenario in which the nodes in one network require support from nodes in another network. For an example of infrastructure dependency see Fig. 1.
In mathematical modeling of social networks, link-centric preferential attachment is a node's propensity to re-establish links to nodes it has previously been in contact with in time-varying networks. This preferential attachment model relies on nodes keeping memory of previous neighbors up to the current time.
Robustness, the ability to withstand failures and perturbations, is a critical attribute of many complex systems including complex networks.











