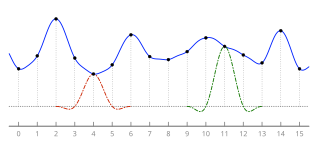
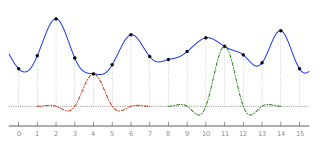
The Nyquist–Shannon sampling theorem is an essential principle for digital signal processing linking the frequency range of a signal and the sample rate required to avoid a type of distortion called aliasing. The theorem states that the sample rate must be at least twice the bandwidth of the signal to avoid aliasing. In practice, it is used to select band-limiting filters to keep aliasing below an acceptable amount when an analog signal is sampled or when sample rates are changed within a digital signal processing function.
The Whittaker–Shannon interpolation formula or sinc interpolation is a method to construct a continuous-time bandlimited function from a sequence of real numbers. The formula dates back to the works of E. Borel in 1898, and E. T. Whittaker in 1915, and was cited from works of J. M. Whittaker in 1935, and in the formulation of the Nyquist–Shannon sampling theorem by Claude Shannon in 1949. It is also commonly called Shannon's interpolation formula and Whittaker's interpolation formula. E. T. Whittaker, who published it in 1915, called it the Cardinal series.
In digital signal processing, spatial anti-aliasing is a technique for minimizing the distortion artifacts (aliasing) when representing a high-resolution image at a lower resolution. Anti-aliasing is used in digital photography, computer graphics, digital audio, and many other applications.
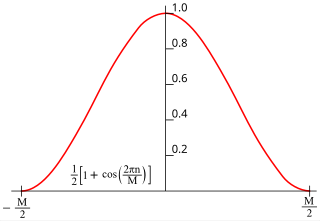
In signal processing and statistics, a window function is a mathematical function that is zero-valued outside of some chosen interval. Typically, windows functions are symmetric around the middle of the interval, approach a maximum in the middle, and taper away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions.
In signal processing, a sinc filter can refer to either a sinc-in-time filter whose impulse response is a sinc function and whose frequency response is rectangular, or to a sinc-in-frequency filter whose impulse response is rectangular and whose frequency response is a sinc function. Calling them according to which domain the filter resembles a sinc avoids confusion. If the domain is unspecified, sinc-in-time is often assumed, or context hopefully can infer the correct domain.

In signal processing, undersampling or bandpass sampling is a technique where one samples a bandpass-filtered signal at a sample rate below its Nyquist rate, but is still able to reconstruct the signal.
In mathematics, the Gibbs phenomenon is the oscillatory behavior of the Fourier series of a piecewise continuously differentiable periodic function around a jump discontinuity. The th partial Fourier series of the function produces large peaks around the jump which overshoot and undershoot the function values. As more sinusoids are used, this approximation error approaches a limit of about 9% of the jump, though the infinite Fourier series sum does eventually converge almost everywhere except points of discontinuity.

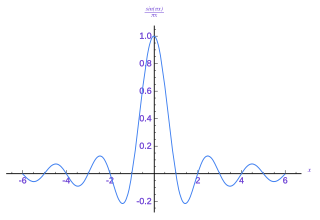
In mathematics, physics and engineering, the sinc function, denoted by sinc(x), has two forms, normalized and unnormalized.
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values.

In digital signal processing, upsampling, expansion, and interpolation are terms associated with the process of resampling in a multi-rate digital signal processing system. Upsampling can be synonymous with expansion, or it can describe an entire process of expansion and filtering (interpolation). When upsampling is performed on a sequence of samples of a signal or other continuous function, it produces an approximation of the sequence that would have been obtained by sampling the signal at a higher rate. For example, if compact disc audio at 44,100 samples/second is upsampled by a factor of 5/4, the resulting sample-rate is 55,125.

In mathematics, bicubic interpolation is an extension of cubic spline interpolation for interpolating data points on a two-dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation. Bicubic interpolation can be accomplished using either Lagrange polynomials, cubic splines, or cubic convolution algorithm.
In a mixed-signal system, a reconstruction filter, sometimes called an anti-imaging filter, is used to construct a smooth analog signal from a digital input, as in the case of a digital to analog converter (DAC) or other sampled data output device.

In computer graphics and digital imaging, imagescaling refers to the resizing of a digital image. In video technology, the magnification of digital material is known as upscaling or resolution enhancement.
Sample-rate conversion, sampling-frequency conversion or resampling is the process of changing the sampling rate or sampling frequency of a discrete signal to obtain a new discrete representation of the underlying continuous signal. Application areas include image scaling and audio/visual systems, where different sampling rates may be used for engineering, economic, or historical reasons.
In the areas of computer vision, image analysis and signal processing, the notion of scale-space representation is used for processing measurement data at multiple scales, and specifically enhance or suppress image features over different ranges of scale. A special type of scale-space representation is provided by the Gaussian scale space, where the image data in N dimensions is subjected to smoothing by Gaussian convolution. Most of the theory for Gaussian scale space deals with continuous images, whereas one when implementing this theory will have to face the fact that most measurement data are discrete. Hence, the theoretical problem arises concerning how to discretize the continuous theory while either preserving or well approximating the desirable theoretical properties that lead to the choice of the Gaussian kernel. This article describes basic approaches for this that have been developed in the literature.
The zero-order hold (ZOH) is a mathematical model of the practical signal reconstruction done by a conventional digital-to-analog converter (DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.
In digital signal processing, a cascaded integrator–comb (CIC) is a computationally efficient class of low-pass finite impulse response (FIR) filter that chains N number of integrator and comb filter pairs to form a decimator or interpolator. In a decimating CIC, the input signal is first fed through N integrator stages, followed by a down-sampler, and then N comb stages. An interpolating CIC has the reverse order of this architecture, but with the down-sampler replaced with a zero-stuffer (up-sampler).
In numerical analysis, multivariate interpolation is interpolation on functions of more than one variable ; when the variates are spatial coordinates, it is also known as spatial interpolation.
A digital delay line is a discrete element in a digital filter, which allows a signal to be delayed by a number of samples. Delay lines are commonly used to delay audio signals feeding loudspeakers to compensate for the speed of sound in air, and to align video signals with accompanying audio, called audio-to-video synchronization. Delay lines may compensate for electronic processing latency so that multiple signals leave a device simultaneously despite having different pathways.

In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from percussion instruments; most noticeable are the pre-echos. The term "ringing" is because the output signal oscillates at a fading rate around a sharp transition in the input, similar to a bell after being struck. As with other artifacts, their minimization is a criterion in filter design.