
In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the relative order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.
In computer science, a fusion tree is a type of tree data structure that implements an associative array on w-bit integers on a finite universe, where each of the input integers has size less than 2w and is non-negative. When operating on a collection of n key–value pairs, it uses O(n) space and performs searches in O(logwn) time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of w. It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard.
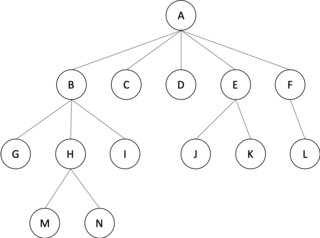
In graph theory, an m-ary tree is an arborescence in which each node has no more than m children. A binary tree is the special case where m = 2, and a ternary tree is another case with m = 3 that limits its children to three.
Intuitively, an algorithmically random sequence is a sequence of binary digits that appears random to any algorithm running on a universal Turing machine. The notion can be applied analogously to sequences on any finite alphabet. Random sequences are key objects of study in algorithmic information theory.

Data parallelism is parallelization across multiple processors in parallel computing environments. It focuses on distributing the data across different nodes, which operate on the data in parallel. It can be applied on regular data structures like arrays and matrices by working on each element in parallel. It contrasts to task parallelism as another form of parallelism.
The block Wiedemann algorithm for computing kernel vectors of a matrix over a finite field is a generalization by Don Coppersmith of an algorithm due to Doug Wiedemann.
Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size s from the n-element sequence, and determining the range of the buckets by sorting the sample and choosing p−1 < s elements from the result. These elements then divide the array into p approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.

A Fenwick tree or binary indexed tree(BIT) is a data structure that can efficiently update values and calculate prefix sums in an array of values.
Collective operations are building blocks for interaction patterns, that are often used in SPMD algorithms in the parallel programming context. Hence, there is an interest in efficient realizations of these operations.
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or expected search time) for a given sequence of accesses (or access probabilities). Optimal BSTs are generally divided into two types: static and dynamic.
In computer science, parallel tree contraction is a broadly applicable technique for the parallel solution of a large number of tree problems, and is used as an algorithm design technique for the design of a large number of parallel graph algorithms. Parallel tree contraction was introduced by Gary L. Miller and John H. Reif, and has subsequently been modified to improve efficiency by X. He and Y. Yesha, Hillel Gazit, Gary L. Miller and Shang-Hua Teng and many others.
In computer science, the reduction operator is a type of operator that is commonly used in parallel programming to reduce the elements of an array into a single result. Reduction operators are associative and often commutative. The reduction of sets of elements is an integral part of programming models such as Map Reduce, where a reduction operator is applied (mapped) to all elements before they are reduced. Other parallel algorithms use reduction operators as primary operations to solve more complex problems. Many reduction operators can be used for broadcasting to distribute data to all processors.
The two-tree broadcast is an algorithm that implements a broadcast communication pattern on a distributed system using message passing. A broadcast is a commonly used collective operation that sends data from one processor to all other processors. The two-tree broadcast communicates concurrently over two binary trees that span all processors. This achieves full usage of the bandwidth in the full-duplex communication model while having a startup latency logarithmic in the number of partaking processors. The algorithm can also be adapted to perform a reduction or prefix sum.
A central problem in algorithmic graph theory is the shortest path problem. Hereby, the problem of finding the shortest path between every pair of nodes is known as all-pair-shortest-paths (APSP) problem. As sequential algorithms for this problem often yield long runtimes, parallelization has shown to be beneficial in this field. In this article two efficient algorithms solving this problem are introduced.
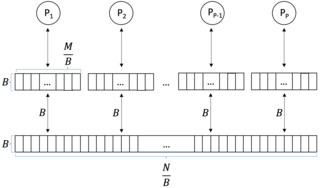
In computer science, a parallel external memory (PEM) model is a cache-aware, external-memory abstract machine. It is the parallel-computing analogy to the single-processor external memory (EM) model. In a similar way, it is the cache-aware analogy to the parallel random-access machine (PRAM). The PEM model consists of a number of processors, together with their respective private caches and a shared main memory.
-dimensional hypercube is a network topology for parallel computers with processing elements. The topology allows for an efficient implementation of some basic communication primitives such as Broadcast, All-Reduce, and Prefix sum. The processing elements are numbered through . Each processing element is adjacent to processing elements whose numbers differ in one and only one bit. The algorithms described in this page utilize this structure efficiently.














































