In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

In graph theory, an isomorphism of graphsG and H is a bijection between the vertex sets of G and H
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the distance being used to define this matrix may or may not be a metric. If there are N elements, this matrix will have size N×N. In graph-theoretic applications the elements are more often referred to as points, nodes or vertices.
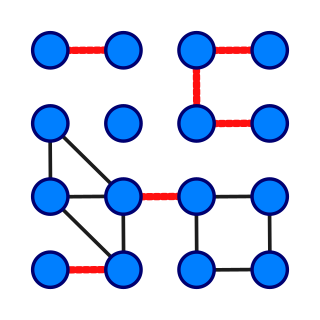
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.

In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.
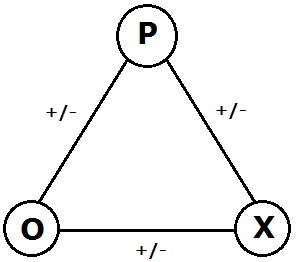
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.
In constraint satisfaction, a decomposition method translates a constraint satisfaction problem into another constraint satisfaction problem that is binary and acyclic. Decomposition methods work by grouping variables into sets, and solving a subproblem for each set. These translations are done because solving binary acyclic problems is a tractable problem.

Assortativity, or assortative mixing is a preference for a network's nodes to attach to others that are similar in some way. Though the specific measure of similarity may vary, network theorists often examine assortativity in terms of a node's degree. The addition of this characteristic to network models more closely approximates the behaviors of many real world networks.

Triadic closure is a concept in social network theory, first suggested by German sociologist Georg Simmel in his 1908 book Soziologie [Sociology: Investigations on the Forms of Sociation]. Triadic closure is the property among three nodes A, B, and C, that if the connections A-B and B-C exist, there is a tendency for the new connection A-C to be formed. Triadic closure can be used to understand and predict the growth of networks, although it is only one of many mechanisms by which new connections are formed in complex networks.

In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.

In combinatorial mathematics, a separable permutation is a permutation that can be obtained from the trivial permutation 1 by direct sums and skew sums. Separable permutations may be characterized by the forbidden permutation patterns 2413 and 3142; they are also the permutations whose permutation graphs are cographs and the permutations that realize the series-parallel partial orders. It is possible to test in polynomial time whether a given separable permutation is a pattern in a larger permutation, or to find the longest common subpattern of two separable permutations.
In graph theory, a partial cube is a graph that is isometric to a subgraph of a hypercube. In other words, a partial cube can be identified with a subgraph of a hypercube in such a way that the distance between any two vertices in the partial cube is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding of the partial cube into a hypercube.
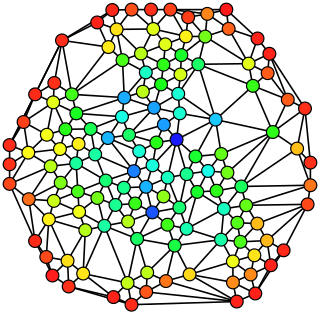
In graph theory, betweenness centrality is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through or the sum of the weights of the edges is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex.
In the mathematics of infinite graphs, an end of a graph represents, intuitively, a direction in which the graph extends to infinity. Ends may be formalized mathematically as equivalence classes of infinite paths, as havens describing strategies for pursuit-evasion games on the graph, or as topological ends of topological spaces associated with the graph.
In discrete mathematics and theoretical computer science, the rotation distance between two binary trees with the same number of nodes is the minimum number of tree rotations needed to reconfigure one tree into another. Because of a combinatorial equivalence between binary trees and triangulations of convex polygons, rotation distance is equivalent to the flip distance for triangulations of convex polygons.
In network theory, link prediction is the problem of predicting the existence of a link between two entities in a network. Examples of link prediction include predicting friendship links among users in a social network, predicting co-authorship links in a citation network, and predicting interactions between genes and proteins in a biological network. Link prediction can also have a temporal aspect, where, given a snapshot of the set of links at time , the goal is to predict the links at time . Link prediction is widely applicable. In e-commerce, link prediction is often a subtask for recommending items to users. In the curation of citation databases, it can be used for record deduplication. In bioinformatics, it has been used to predict protein-protein interactions (PPI). It is also used to identify hidden groups of terrorists and criminals in security related applications.
Blockmodeling refers to a set or a coherent framework, that is used for analyzing social structure and also for setting procedure(s) for partitioning (clustering) social network's units, based on specific patterns, which form a distinctive structure through interconnectivity. It is primarily used in statistics, machine learning, and network science.













