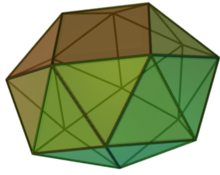
In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices.

In geometry, the gyroelongated square pyramid is the Johnson solid that can be constructed by attaching an equilateral square pyramid to a square antiprism. It occurs in the chemistry such as square antiprismatic molecular geometry.

In geometry, the elongated pentagonal pyramid is one of the Johnson solids. As the name suggests, it can be constructed by elongating a pentagonal pyramid by attaching a pentagonal prism to its base.

In geometry, the gyroelongated square cupola is one of the Johnson solids (J23). As the name suggests, it can be constructed by gyroelongating a square cupola (J4) by attaching an octagonal antiprism to its base. It can also be seen as a gyroelongated square bicupola (J45) with one square bicupola removed.

In geometry, the pentagonal cupola is one of the Johnson solids. It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.

In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.

In geometry, the hebesphenomegacorona is one of the Johnson solids. It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids. It has 21 faces, 18 triangles and 3 squares, 33 edges, and 14 vertices.

In geometry, the sphenomegacorona is one of the Johnson solids. It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.

In geometry, the sphenocorona is one of the Johnson solids. It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.

In geometry, the triangular hebesphenorotunda is one of the Johnson solids.

In geometry, the augmented sphenocorona is the Johnson solid that can be constructed by attaching an equilateral square pyramid to one of the square faces of the sphenocorona. It is the only Johnson solid arising from "cut and paste" manipulations where the components are not all prisms, antiprisms or sections of Platonic or Archimedean solids.

In geometry, the elongated triangular bipyramid or triakis triangular prism is one of the Johnson solids, convex polyhedra whose faces are regular polygons. As the name suggests, it can be constructed by elongating a triangular bipyramid by inserting a triangular prism between its congruent halves.

In geometry, the gyrobifastigium is the 26th Johnson solid. It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a quarter-turn to one prism. It is the only Johnson solid that can tile three-dimensional space.

In geometry, the gyroelongated pentagonal bicupola is one of the Johnson solids. As the name suggests, it can be constructed by gyroelongating a pentagonal bicupola by inserting a decagonal antiprism between its congruent halves.

In geometry, the elongated triangular cupola is one of the Johnson solids. As the name suggests, it can be constructed by elongating a triangular cupola by attaching a hexagonal prism to its base.
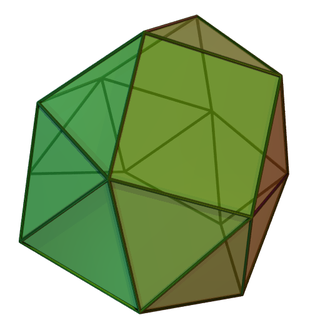
In geometry, the gyroelongated triangular cupola is one of the Johnson solids (J22). It can be constructed by attaching a hexagonal antiprism to the base of a triangular cupola (J3). This is called "gyroelongation", which means that an antiprism is joined to the base of a solid, or between the bases of more than one solid.

In geometry, the gyroelongated triangular bicupola is one of the Johnson solids. As the name suggests, it can be constructed by gyroelongating a triangular bicupola by inserting a hexagonal antiprism between its congruent halves.

In geometry, the gyroelongated pentagonal cupolarotunda is one of the Johnson solids. As the name suggests, it can be constructed by gyroelongating a pentagonal cupolarotunda by inserting a decagonal antiprism between its two halves.