Definition
Vibronic coupling describes the mixing of different electronic states as a result of small vibrations.
| Coupling in science |
|---|
| Classical coupling |
| Quantum coupling |
Vibronic coupling (also called nonadiabatic coupling or derivative coupling) in a molecule involves the interaction between electronic and nuclear vibrational motion. [1] [2] The term "vibronic" originates from the combination of the terms "vibrational" and "electronic", denoting the idea that in a molecule, vibrational and electronic interactions are interrelated and influence each other. The magnitude of vibronic coupling reflects the degree of such interrelation.
In theoretical chemistry, the vibronic coupling is neglected within the Born–Oppenheimer approximation. Vibronic couplings are crucial to the understanding of nonadiabatic processes, especially near points of conical intersections. [3] [4] The direct calculation of vibronic couplings used to be uncommon due to difficulties associated with its evaluation, but has recently gained popularity due to increased interest in the quantitative prediction of internal conversion rates, as well as the development of cheap but rigorous ways to analytically calculate the vibronic couplings, especially at the TDDFT level. [5] [6] [7]
Vibronic coupling describes the mixing of different electronic states as a result of small vibrations.
The evaluation of vibronic coupling often involves complex mathematical treatment.
The form of vibronic coupling is essentially the derivative of the wave function. Each component of the vibronic coupling vector can be calculated with numerical differentiation methods using wave functions at displaced geometries. This is the procedure used in MOLPRO. [8]
First order accuracy can be achieved with forward difference formula:
Second order accuracy can be achieved with central difference formula:
Here, is a unit vector along direction . is the transition density between the two electronic states.
Evaluation of electronic wave functions for both electronic states are required at N displacement geometries for first order accuracy and 2*N displacements to achieve second order accuracy, where N is the number of nuclear degrees of freedom. This can be extremely computationally demanding for large molecules.
As with other numerical differentiation methods, the evaluation of nonadiabatic coupling vector with this method is numerically unstable, limiting the accuracy of the result. Moreover, the calculation of the two transition densities in the numerator are not straightforward. The wave functions of both electronic states are expanded with Slater determinants or configuration state functions (CSF). The contribution from the change of CSF basis is too demanding to evaluate using numerical method, and is usually ignored by employing an approximate diabatic CSF basis. This will also cause further inaccuracy of the calculated coupling vector, although this error is usually tolerable.
Evaluating derivative couplings with analytic gradient methods has the advantage of high accuracy and very low cost, usually much cheaper than one single point calculation. This means an acceleration factor of 2N. However, the process involves intense mathematical treatment and programming. As a result, few programs have currently implemented analytic evaluation of vibronic couplings at wave function theory levels. Details about this method can be found in ref. [9] For the implementation for SA-MCSCF and MRCI in COLUMBUS, please see ref. [10]
The computational cost of evaluating the vibronic coupling using (multireference) wave function theory has led to the idea of evaluating them at the TDDFT level, which indirectly describes the excited states of a system without describing its excited state wave functions. However, the derivation of the TDDFT vibronic coupling theory is not trivial, since there are no electronic wave functions in TDDFT that are available for plugging into the defining equation of the vibronic coupling. [5]
In 2000, Chernyak and Mukamel [11] showed that in the complete basis set (CBS) limit, knowledge of the reduced transition density matrix between a pair of states (both at the unperturbed geometry) suffices to determine the vibronic couplings between them. The vibronic couplings between two electronic states are given by contracting their reduced transition density matrix with the geometric derivatives of the nuclear attraction operator, followed by dividing by the energy difference of the two electronic states:
This enables one to calculate the vibronic couplings at the TDDFT level, since although TDDFT does not give excited state wave functions, it does give reduced transition density matrices, not only between the ground state and an excited state, but also between two excited states. The proof of the Chernyak-Mukamel formula is straightforward and involves the Hellmann-Feynman theorem. While the formula provides useful accuracy for a plane-wave basis (see e.g. ref. [12] ), it converges extremely slowly with respect to the basis set if an atomic orbital basis set is used, due to the neglect of the Pulay force. Therefore, modern implementations in molecular codes typically use expressions that include the Pulay force contributions, derived from the Lagrangian formalism. [5] [6] [7] They are more expensive than the Chernyak-Mukamel formula, but still much cheaper than the vibronic couplings at wave function theory levels (more specifically, they are roughly as expensive as the SCF gradient for ground state-excited state vibronic couplings, and as expensive as the TDDFT gradient for excited state-excited state vibronic couplings). Moreover, they are much more accurate than the Chernyak-Mukamel formula for realistically sized atomic orbital basis sets. [5]
Vibronic coupling is large in the case of two adiabatic potential energy surfaces coming close to each other (that is, when the energy gap between them is of the order of magnitude of one oscillation quantum). This happens in the neighbourhood of an avoided crossing of potential energy surfaces corresponding to distinct electronic states of the same spin symmetry. At the vicinity of conical intersections, where the potential energy surfaces of the same spin symmetry cross, the magnitude of vibronic coupling approaches infinity. In either case the adiabatic or Born–Oppenheimer approximation fails and vibronic couplings have to be taken into account.
The large magnitude of vibronic coupling near avoided crossings and conical intersections allows wave functions to propagate from one adiabatic potential energy surface to another, giving rise to nonadiabatic phenomena such as radiationless decay. Therefore, one of the most important applications of vibronic couplings is the quantitative calculation of internal conversion rates, through e.g. nonadiabatic molecular dynamics [13] (including but not limited to surface hopping and path integral molecular dynamics). When the potential energy surfaces of both the initial and the final electronic state are approximated by multidimensional harmonic oscillators, one can compute the internal conversion rate by evaluating the vibration correlation function, which is much cheaper than nonadiabatic molecular dynamics and is free from random noise; this gives a fast method to compute the rates of relatively slow internal conversion processes, for which nonadiabatic molecular dynamics methods are not affordable. [14]
The singularity of vibronic coupling at conical intersections is responsible for the existence of Geometric phase, which was discovered by Longuet-Higgins [15] in this context. Geometric phase around the conical intersection involving the ground electronic state of the C6H3F3+ molecular ion is discussed on pages 385-386 of the textbook by Bunker and Jensen. [16]
Although crucial to the understanding of nonadiabatic processes, direct evaluation of vibronic couplings has been very limited until very recently.
Evaluation of vibronic couplings is often associated with severe difficulties in mathematical formulation and program implementations. As a result, the algorithms to evaluate vibronic couplings at wave function theory levels, or between two excited states, are not yet implemented in many quantum chemistry program suites. By comparison, vibronic couplings between the ground state and an excited state at the TDDFT level, which are easy to formulate and cheap to calculate, are more widely available.
The evaluation of vibronic couplings typically requires correct description of at least two electronic states in regions where they are strongly coupled. This usually requires the use of multi-reference methods such as MCSCF and MRCI, which are computationally demanding and delicate quantum-chemical methods. However, there are also applications where vibronic couplings are needed but the relevant electronic states are not strongly coupled, for example when calculating slow internal conversion processes; in this case even methods like TDDFT, which fails near ground state-excited state conical intersections, [17] can give useful accuracy. Moreover, TDDFT can describe the vibronic coupling between two excited states in a qualitatively correct fashion, even if the two excited states are very close in energy and therefore strongly coupled (provided that the equation-of-motion (EOM) variant of the TDDFT vibronic coupling is used in place of the time-dependent perturbation theory (TDPT) variant [5] ). Therefore, the unsuitability of TDDFT for calculating ground state-excited state vibronic couplings near a ground state-excited state conical intersection can be bypassed by choosing a third state as the reference state of the TDDFT calculation (i.e. the ground state is treated like an excited state), leading to the popular approach of using spin-flip TDDFT to evaluate ground state-excited state vibronic couplings. [18] When even an approximate calculation is unrealistic, the magnitude of vibronic coupling is often introduced as an empirical parameter determined by reproducing experimental data.
Alternatively, one can avoid explicit use of derivative couplings by switch from the adiabatic to the diabatic representation of the potential energy surfaces. Although rigorous validation of a diabatic representation requires knowledge of vibronic coupling, it is often possible to construct such diabatic representations by referencing the continuity of physical quantities such as dipole moment, charge distribution or orbital occupations. However, such construction requires detailed knowledge of a molecular system and introduces significant arbitrariness. Diabatic representations constructed with different method can yield different results and the reliability of the result relies on the discretion of the researcher.
The first discussion of the effect of vibronic coupling on molecular spectra is given in the paper by Herzberg and Teller. [19] Although the Herzberg–Teller effect appears to be the result of either vibronic coupling or the dependence of the electronic transition moment on the nuclear coordinates, it can be shown that these two apparently different causes of the Herzberg–Teller effect in a spectrum are two manifestations of the same phenomenon (see Section 14.1.9 of the book by Bunker and Jensen [16] ). Calculations of the lower excited levels of benzene by Sklar in 1937 (with the valence bond method) and later in 1938 by Goeppert-Mayer and Sklar (with the molecular orbital method) demonstrated a correspondence between the theoretical predictions and experimental results of the benzene spectrum. The benzene spectrum was the first qualitative computation of the efficiencies of various vibrations at inducing intensity absorption. [20]
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of molecules, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense ferment in the development of quantum mechanics.
In classical and quantum mechanics, geometric phase is a phase difference acquired over the course of a cycle, when a system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian. The phenomenon was independently discovered by S. Pancharatnam (1956), in classical optics and by H. C. Longuet-Higgins (1958) in molecular physics; it was generalized by Michael Berry in (1984). It is also known as the Pancharatnam–Berry phase, Pancharatnam phase, or Berry phase. It can be seen in the conical intersection of potential energy surfaces and in the Aharonov–Bohm effect. Geometric phase around the conical intersection involving the ground electronic state of the C6H3F3+ molecular ion is discussed on pages 385–386 of the textbook by Bunker and Jensen. In the case of the Aharonov–Bohm effect, the adiabatic parameter is the magnetic field enclosed by two interference paths, and it is cyclic in the sense that these two paths form a loop. In the case of the conical intersection, the adiabatic parameters are the molecular coordinates. Apart from quantum mechanics, it arises in a variety of other wave systems, such as classical optics. As a rule of thumb, it can occur whenever there are at least two parameters characterizing a wave in the vicinity of some sort of singularity or hole in the topology; two parameters are required because either the set of nonsingular states will not be simply connected, or there will be nonzero holonomy.
The Jahn–Teller effect is an important mechanism of spontaneous symmetry breaking in molecular and solid-state systems which has far-reaching consequences in different fields, and is responsible for a variety of phenomena in spectroscopy, stereochemistry, crystal chemistry, molecular and solid-state physics, and materials science. The effect is named for Hermann Arthur Jahn and Edward Teller, who first reported studies about it in 1937.
One of the guiding principles in modern chemical dynamics and spectroscopy is that the motion of the nuclei in a molecule is slow compared to that of its electrons. This is justified by the large disparity between the mass of an electron, and the typical mass of a nucleus and leads to the Born–Oppenheimer approximation and the idea that the structure and dynamics of a chemical species are largely determined by nuclear motion on potential energy surfaces.
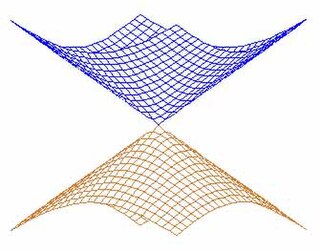
In quantum chemistry, a conical intersection of two or more potential energy surfaces is the set of molecular geometry points where the potential energy surfaces are degenerate (intersect) and the non-adiabatic couplings between these states are non-vanishing. In the vicinity of conical intersections, the Born–Oppenheimer approximation breaks down and the coupling between electronic and nuclear motion becomes important, allowing non-adiabatic processes to take place. The location and characterization of conical intersections are therefore essential to the understanding of a wide range of important phenomena governed by non-adiabatic events, such as photoisomerization, photosynthesis, vision and the photostability of DNA. The conical intersection involving the ground electronic state potential energy surface of the C6H3F3+ molecular ion is discussed in connection with the Jahn–Teller effect in Section 13.4.2 on pages 380-388 of the textbook by Bunker and Jensen.

MOLCAS is an ab initio computational chemistry program, developed as a joint project by a number of international institutes. MOLCAS is developed by scientists to be used by scientists. It is not primarily a commercial product and it is not sold in order to produce a fortune for its owner.
The COLUMBUS PROGRAMS are a computational chemistry software suite for calculating ab initio molecular electronic structures, designed as a collection of individual programs communicating through files. The programs focus on extended multi-reference calculations of atomic and molecular ground and excited states. In addition to standard classes of reference wave functions such as CAS and RAS, calculations can be performed with selected configurations. Some features employ the atomic orbital integrals and gradient routines from the Dalton as well as MOLCAS program suites. COLUMBUS is distributed open-source under the LGPL license.
Octopus is a software package for performing Kohn–Sham density functional theory (DFT) and time-dependent density functional theory (TDDFT) calculations.
The Born–Huang approximation is an approximation closely related to the Born–Oppenheimer approximation. It takes into account diagonal nonadiabatic effects in the electronic Hamiltonian better than the Born–Oppenheimer approximation. Despite the addition of correction terms, the electronic states remain uncoupled under the Born–Huang approximation, making it an adiabatic approximation.
Car–Parrinello molecular dynamics or CPMD refers to either a method used in molecular dynamics or the computational chemistry software package used to implement this method.

The Landau–Zener formula is an analytic solution to the equations of motion governing the transition dynamics of a two-state quantum system, with a time-dependent Hamiltonian varying such that the energy separation of the two states is a linear function of time. The formula, giving the probability of a diabatic transition between the two energy states, was published separately by Lev Landau, Clarence Zener, Ernst Stueckelberg, and Ettore Majorana, in 1932.
In computational chemistry, spin contamination is the artificial mixing of different electronic spin-states. This can occur when an approximate orbital-based wave function is represented in an unrestricted form – that is, when the spatial parts of α and β spin-orbitals are permitted to differ. Approximate wave functions with a high degree of spin contamination are undesirable. In particular, they are not eigenfunctions of the total spin-squared operator, Ŝ2, but can formally be expanded in terms of pure spin states of higher multiplicities.
Surface hopping is a mixed quantum-classical technique that incorporates quantum mechanical effects into molecular dynamics simulations. Traditional molecular dynamics assume the Born-Oppenheimer approximation, where the lighter electrons adjust instantaneously to the motion of the nuclei. Though the Born-Oppenheimer approximation is applicable to a wide range of problems, there are several applications, such as photoexcited dynamics, electron transfer, and surface chemistry where this approximation falls apart. Surface hopping partially incorporates the non-adiabatic effects by including excited adiabatic surfaces in the calculations, and allowing for 'hops' between these surfaces, subject to certain criteria.

Newton-X is a general program for molecular dynamics simulations beyond the Born-Oppenheimer approximation. It has been primarily used for simulations of ultrafast processes in photoexcited molecules. It has also been used for simulation of band envelops of absorption and emission spectra.
SHARC is an ab initio molecular dynamics program suite primarily dedicated to study the excited-state dynamics of molecules. It is free for academic use, open source released under the GNU General Public License.
The pseudo Jahn–Teller effect (PJTE), occasionally also known as second-order JTE, is a direct extension of the Jahn–Teller effect (JTE) where spontaneous symmetry breaking in polyatomic systems occurs even in nondegenerate electronic states under the influence of sufficiently low-lying excited states of appropriate symmetry. "The pseudo Jahn–Teller effect is the only source of instability and distortions of high-symmetry configurations of polyatomic systems in nondegenerate states, and it contributes significantly to the instability in degenerate states".
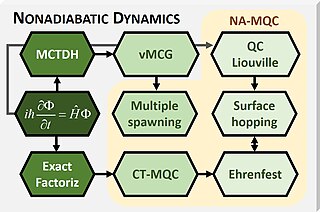
Mixed quantum-classical (MQC) dynamics is a class of computational theoretical chemistry methods tailored to simulate non-adiabatic (NA) processes in molecular and supramolecular chemistry. Such methods are characterized by:
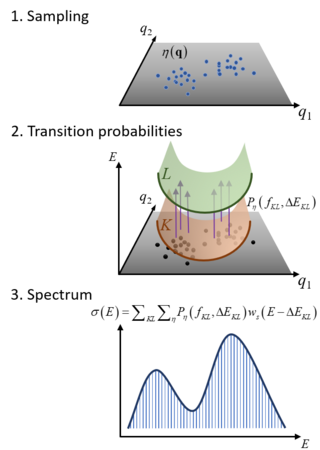
The Nuclear Ensemble Approach (NEA) is a general method for simulations of diverse types of molecular spectra. It works by sampling an ensemble of molecular conformations in the source state, computing the transition probabilities to the target states for each of these geometries, and performing a sum over all these transitions convoluted with shape function. The result is an incoherent spectrum containing absolute band shapes through inhomogeneous broadening.

Isaac B. Bersuker is a Soviet-Moldоvan-American theoretical physicist and quantum chemist whose principal research is in chemical physics, solid-state physics, and theoretical chemistry. Known for his "life-long years of experience in theoretical chemistry" working on the electronic structure and properties of coordination compounds, Isaac B. Bersuker is “one of the most widely recognized authorities” in the theory of the Jahn–Teller effect (JTE) and the pseudo-Jahn–Teller effect (PJTE). His accomplishments include explaining the polarization of the atomic core in Rydberg atoms, the effect of tunneling splitting in molecules and solids with a strong JTE, and the discovery of the PJTE origin of ferroelectricity in cubic perovskites. Known as the leading expert in JTE and PJTE, Bersuker is the permanent chairman of the international steering committee of the Jahn–Teller symposia. His present affiliation is with the Oden Institute for Computational Engineering and Science of the Department of Chemistry of the University of Texas at Austin.