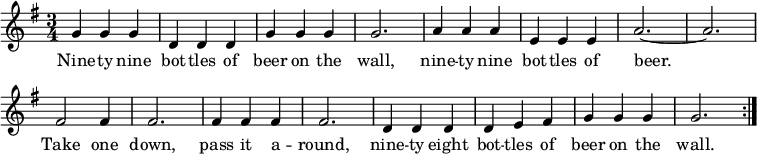"99 Bottles of Beer" or "100 Bottles of Pop on the Wall" is a traditional reverse counting song in the United States and Canada. It is popular to sing on road trips, as it has a very repetitive format which is easy to memorize and can take a long time when sung in full. In particular, the song is often sung by children on long school bus trips, such as class field trips, or on Scout or Girl Guide outings.
The song is a variation of a 19th century college students' song "Forty-nine Blue Bottles a-Hangin' on the Wall" or simply "Forty-nine Bottles Hanging on the Wall". [1] The melody and lyrics are recorded in a college songbook from 1890 [2] as:[ failed verification ]
By 1898, a variation existed with the modern bottle count of 99 and the bottles specified as beer bottles. [3] [ failed verification ]
The song's lyrics are as follows, beginning with n=99: [4] [5]
(n) bottles of beer on the wall.
(n) bottles of beer.
Take one down, pass it around,
(n-1) bottles of beer on the wall.
The same verse is repeated, each time with one bottle fewer, until there is none left. Variations on the last verse following the last bottle going down include lines such as:
No more bottles of beer on the wall,
no more bottles of beer.
Go to the store and buy some more,
99 bottles of beer on the wall...
Or:
No more bottles of beer on the wall,
no more bottles of beer.
We've taken them down
and passed them around;
now we're drunk and passed out!
Other alternate lines read:
If that one bottle should happen to fall,
what a waste of alcohol!
Or:
No more bottles of beer on the wall,
no more bottles of beer.
There's nothing else to fall,
because there's no more bottles of beer on the wall.
Or the song does not stop at the last "1" or "0" bottles of beer but continues counting with −1 (Negative one) Bottles of beer on the wall Take one down, pass it around, −2 (negative 2) bottles of beer on the wall... continuing onward through the negative numbers.
Singing all verses takes an extraordinary long time. The American comedian Andy Kaufman used this for comedic effect early in his career when he actually sang all 100 verses. [7]
Atticus, a band from Knoxville, Tennessee, recorded a thirteen and a half minute live version of the song in its entirety at the Glasgow Cathouse in Scotland. It was included in the 2001 album Figment. Rich Stewart aka Homebrew Stew listed it as the number one drinking song out of 86 in an article for Modern Drunkard Magazine the following year. [8]
Donald Byrd has collected dozens of variants inspired by mathematical concepts and written by himself and others. [9] (A subset of his collection has been published. [10] ) Byrd argues that the collection has pedagogic as well as amusement value. Among his variants are:
Other versions in Byrd's collection involve concepts including geometric progressions, differentials, Euler's identity, complex numbers, summation notation, the Cantor set, the Fibonacci sequence, and the continuum hypothesis, among others.
The computer scientist Donald Knuth proved that the song has a complexity of in his in-joke-article "The Complexity of Songs". [11]
Numerous computer programs exist to output the lyrics to the song. This is analogous to "Hello, World!" programs, with the addition of a loop. As with "Hello World!", this can be a practice exercise for those studying computer programming, and a demonstration of different programming paradigms dealing with looping constructs and syntactic differences between programming languages within a paradigm.
The program has been written in over 1,500 different programming languages. [12]
#include<stdio.h>intmain(void){for(size_ti=99;i>0;i--){printf("%zu bottle%s of beer on the wall, %zu bottle%s of beer.\nTake one down & pass it around, now there's ",i,(i==1?"":"s"),i,(i==1?"":"s"));printf((i>1)?"%zu bottle%s of beer on the wall\n":"no more bottles of beer on the wall!\n",i-1,i==2?"":"s");}}fnmain(){foriin(3..100).rev(){println!("{i} bottles of beer on the wall, {i} bottles of beer.\nTake one down and pass it around, now there's {} more bottles of beer on the wall!",(i-1));}println!("2 bottles of beer on the wall, 2 bottles of beer.\nTake one down and pass it around, now there's 1 more bottle of beer on the wall!",);println!("1 bottle of beer on the wall, 1 bottle of beer.\nTake one down and pass it around, there's no more bottles of beer on the wall!");}verses::[String]verses="1 bottle of beer on the wall, 1 bottle of beer.\nTake one down and pass it around, there's no more bottles of beer on the wall!":"2 bottles of beer on the wall, 2 bottles of beer.\nTake one down and pass it around, now there's 1 more bottle of beer on the wall!":map(\n->shown++" bottles of beer on the wall, "++shown++" bottles of beer.\nTake one down and pass it around, now there's "++show(n-1)++" more bottles of beer on the wall!")[3..]main::IO()main=mapM_putStrLn(reverse$take99verses)In mathematics, specifically set theory, the continuum hypothesis is a hypothesis about the possible sizes of infinite sets. It states that
there is no set whose cardinality is strictly between that of the integers and the real numbers,
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is countable if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements.
In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter (aleph) marked with subscript indicating their rank among the infinite cardinals.
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.
Georg Ferdinand Ludwig Philipp Cantor was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
In mathematical analysis, a null set is a Lebesgue measurable set of real numbers that has measure zero. This can be characterized as a set that can be covered by a countable union of intervals of arbitrarily small total length.
In mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than aleph-null, the cardinality of the natural numbers.
In mathematics, transfinite numbers or infinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets. The term transfinite was coined in 1895 by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these objects, which were, nevertheless, not finite. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term transfinite also remains in use.
In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets that can be well-ordered. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Hebrew letter aleph.
In mathematics, two sets or classes A and B are equinumerous if there exists a one-to-one correspondence (or bijection) between them, that is, if there exists a function from A to B such that for every element y of B, there is exactly one element x of A with f(x) = y. Equinumerous sets are said to have the same cardinality (number of elements). The study of cardinality is often called equinumerosity (equalness-of-number). The terms equipollence (equalness-of-strength) and equipotence (equalness-of-power) are sometimes used instead.
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. More explicitly, this means that is a regular cardinal if and only if every unbounded subset has cardinality . Infinite well-ordered cardinals that are not regular are called singular cardinals. Finite cardinal numbers are typically not called regular or singular.
In mathematics, particularly in set theory, the beth numbers are a certain sequence of infinite cardinal numbers, conventionally written , where is the Hebrew letter beth. The beth numbers are related to the aleph numbers, but unless the generalized continuum hypothesis is true, there are numbers indexed by that are not indexed by .
Aldor is a programming language. It is the successor of A# as the extension language of the Axiom computer algebra system.
In set theory, the cardinality of the continuum is the cardinality or "size" of the set of real numbers , sometimes called the continuum. It is an infinite cardinal number and is denoted by or .
In mathematics, set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological questions that are independent of Zermelo–Fraenkel set theory (ZFC).
In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.
Intuitively, an algorithmically random sequence is a sequence of binary digits that appears random to any algorithm running on a universal Turing machine. The notion can be applied analogously to sequences on any finite alphabet. Random sequences are key objects of study in algorithmic information theory.
This article contains a discussion of paradoxes of set theory. As with most mathematical paradoxes, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradictions within modern axiomatic set theory.
Infinity is something which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
