
L'Hôpital's rule, also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli.

In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.
In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
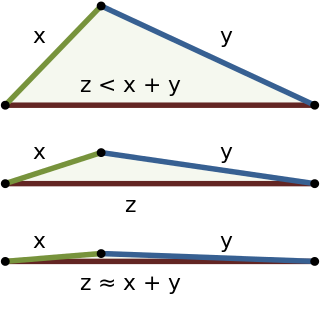
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that

In mathematics and computer science, the floor function is the function that takes as input a real number x, and gives as output the greatest integer less than or equal to x, denoted ⌊x⌋ or floor(x). Similarly, the ceiling function maps x to the least integer greater than or equal to x, denoted ⌈x⌉ or ceil(x).
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem which relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.
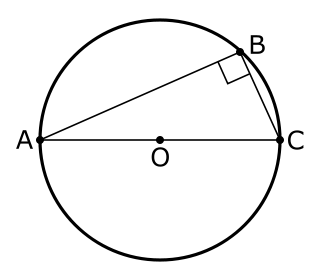
In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In calculus, the squeeze theorem is a theorem regarding the limit of a function that is trapped between two other functions.
In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradiction used to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction. It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions.

In probability theory and statistics, the triangular distribution is a continuous probability distribution with lower limit a, upper limit b and mode c, where a < b and a ≤ c ≤ b.
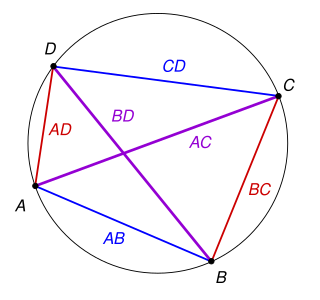
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.

In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the pairwise intersections of three cevians. The theorem states that if in triangle points , , and lie on segments , , and , then writing , , and , the signed area of the triangle formed by the cevians , , and is

In mathematics, De Gua's theorem is a three-dimensional analog of the Pythagorean theorem named after Jean Paul de Gua de Malves. It states that if a tetrahedron has a right-angle corner, then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces:

In geometry, the Steiner inellipse, midpoint inellipse, or midpoint ellipse of a triangle is the unique ellipse inscribed in the triangle and tangent to the sides at their midpoints. It is an example of an inellipse. By comparison the inscribed circle and Mandart inellipse of a triangle are other inconics that are tangent to the sides, but not at the midpoints unless the triangle is equilateral. The Steiner inellipse is attributed by Dörrie to Jakob Steiner, and a proof of its uniqueness is given by Dan Kalman.
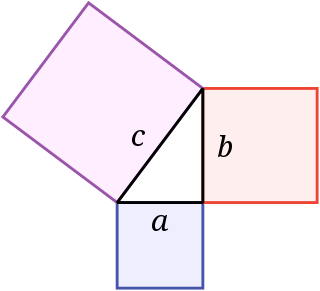
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
In arithmetic combinatorics, the corners theorem states that for every , for large enough , any set of at least points in the grid contains a corner, i.e., a triple of points of the form with . It was first proved by Miklós Ajtai and Endre Szemerédi in 1974 using Szemerédi's theorem. In 2003, József Solymosi gave a short proof using the triangle removal lemma.
In additive combinatorics, the Plünnecke–Ruzsa inequality is an inequality that bounds the size of various sumsets of a set , given that there is another set so that is not much larger than . A slightly weaker version of this inequality was originally proven and published by Helmut Plünnecke (1970). Imre Ruzsa (1989) later published a simpler proof of the current, more general, version of the inequality. The inequality forms a crucial step in the proof of Freiman's theorem.
















