
In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as the rectangular cuboid with six faces are all squares, and parallelepiped with the edges are all equal. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.

In physics and mathematics, the dimension of a mathematical space is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

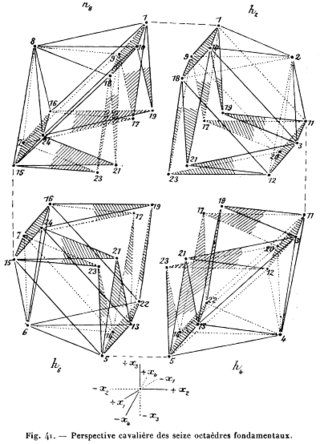
In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.

Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units or by various imperial or US customary units. The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

Charles Howard Hinton was a British mathematician and writer of science fiction works titled Scientific Romances. He was interested in higher dimensions, particularly the fourth dimension. He is known for coining the word "tesseract" and for his work on methods of visualising the geometry of higher dimensions.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible abstraction of the observation that one needs only three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height. This concept of ordinary space is called Euclidean space because it corresponds to Euclid's geometry, which was originally abstracted from the spatial experiences of everyday life.

In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In hyperbolic geometry, the order-4 dodecahedral honeycomb is one of four compact regular space-filling tessellations of hyperbolic 3-space. With Schläfli symbol {5,3,4}, it has four dodecahedra around each edge, and 8 dodecahedra around each vertex in an octahedral arrangement. Its vertices are constructed from 3 orthogonal axes. Its dual is the order-5 cubic honeycomb.

The Octacube is a large, stainless steel sculpture displayed in the mathematics department of Pennsylvania State University in State College, PA. The sculpture represents a mathematical object called the 24-cell or "octacube". Because a real 24-cell is four-dimensional, the artwork is actually a projection into the three-dimensional world.

Crucifixion (Corpus Hypercubus) is a 1954 oil-on-canvas painting by Salvador Dalí. A nontraditional, surrealist portrayal of the Crucifixion, it depicts Christ on a polyhedron net of a tesseract (hypercube). It is one of his best-known paintings from the later period of his career.
Synergetics is the empirical study of systems in transformation, with an emphasis on whole system behaviors unpredicted by the behavior of any components in isolation. R. Buckminster Fuller (1895–1983) named and pioneered the field. His two-volume work Synergetics: Explorations in the Geometry of Thinking, in collaboration with E. J. Applewhite, distills a lifetime of research into book form.

In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron.
New possibilities opened up by the concept of four-dimensional space helped inspire many modern artists in the first half of the twentieth century. Early Cubists, Surrealists, Futurists, and abstract artists took ideas from higher-dimensional mathematics and used them to radically advance their work.
The idea of a fourth dimension has been a factor in the evolution of modern art, but use of concepts relating to higher dimensions has been little discussed by academics in the literary world. From the late 19th century onwards, many writers began to make use of possibilities opened up by the exploration of such concepts as hypercube geometry. While many writers took the fourth dimension to be one of time, others preferred to think of it in spatial terms, and some associated the new mathematics with wider changes in modern culture.

















