
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals.

In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.

In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by , , , , or .

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.
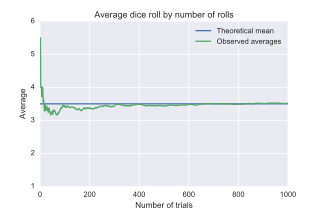
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and tends to become closer to the expected value as more trials are performed.
Covariance in probability theory and statistics is a measure of the joint variability of two random variables.
In probability theory and statistics, two real-valued random variables, , , are said to be uncorrelated if their covariance, , is zero. If two variables are uncorrelated, there is no linear relationship between them.

In probability theory and statistics, a covariance matrix is a square matrix giving the covariance between each pair of elements of a given random vector.

In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy.

Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. The result can be either a continuous or a discrete distribution.
The actuarial present value (APV) is the expected value of the present value of a contingent cash flow stream. Actuarial present values are typically calculated for the benefit-payment or series of payments associated with life insurance and life annuities. The probability of a future payment is based on assumptions about the person's future mortality which is typically estimated using a life table.
Credibility theory is a branch of actuarial mathematics concerned with determining risk premiums. To achieve this, it uses mathematical models in an effort to forecast the (expected) number of insurance claims based on past observations. Technically speaking, the problem is to find the best linear approximation to the mean of the Bayesian predictive density, which is why credibility theory has many results in common with linear filtering as well as Bayesian statistics more broadly.
In mathematics, the Schuette–Nesbitt formula is a generalization of the inclusion–exclusion principle. It is named after Donald R. Schuette and Cecil J. Nesbitt.
In probability theory and statistics, a cross-covariance matrix is a matrix whose element in the i, j position is the covariance between the i-th element of a random vector and j-th element of another random vector. A random vector is a random variable with multiple dimensions. Each element of the vector is a scalar random variable. Each element has either a finite number of observed empirical values or a finite or infinite number of potential values. The potential values are specified by a theoretical joint probability distribution. Intuitively, the cross-covariance matrix generalizes the notion of covariance to multiple dimensions.

In statistics and in probability theory, distance correlation or distance covariance is a measure of dependence between two paired random vectors of arbitrary, not necessarily equal, dimension. The population distance correlation coefficient is zero if and only if the random vectors are independent. Thus, distance correlation measures both linear and nonlinear association between two random variables or random vectors. This is in contrast to Pearson's correlation, which can only detect linear association between two random variables.
Hattendorff's Theorem, attributed to K. Hattendorff (1868), is a theorem in actuarial science that describes the allocation of the variance or risk of the loss random variable over the lifetime of an actuarial reserve. In other words, Hattendorff's theorem demonstrates that the variation in the present value of the loss of an issued insurance policy can be allocated to the future years during which the insured is still alive. This, in turn, facilitates the management of risk prevalent in such insurance contracts over short periods of time.
In investment, an annuity is a series of payments made at equal intervals. Examples of annuities are regular deposits to a savings account, monthly home mortgage payments, monthly insurance payments and pension payments. Annuities can be classified by the frequency of payment dates. The payments (deposits) may be made weekly, monthly, quarterly, yearly, or at any other regular interval of time. Annuities may be calculated by mathematical functions known as "annuity functions".

In probability theory and statistics, a complex random vector is typically a tuple of complex-valued random variables, and generally is a random variable taking values in a vector space over the field of complex numbers. If are complex-valued random variables, then the n-tuple is a complex random vector. Complex random variables can always be considered as pairs of real random vectors: their real and imaginary parts.
A mixed Poisson distribution is a univariate discrete probability distribution in stochastics. It results from assuming that the conditional distribution of a random variable, given the value of the rate parameter, is a Poisson distribution, and that the rate parameter itself is considered as a random variable. Hence it is a special case of a compound probability distribution. Mixed Poisson distributions can be found in actuarial mathematics as a general approach for the distribution of the number of claims and is also examined as an epidemiological model. It should not be confused with compound Poisson distribution or compound Poisson process.























