Affine Grassmannian (manifold)

Last updated September 25, 2021

In mathematics, there are two distinct meanings of the term affine Grassmannian. In one it is the manifold of all k-dimensional affine subspaces of Rⁿ (described on this page), while in the other the affine Grassmannian is a quotient of a group-ring based on formal Laurent series.

Formal definition

Given a finite-dimensional vector space V and a non-negative integer k, then Graff_k(V) is the topological space of all affine k-dimensional subspaces of V.

It has a natural projection p:Graff_k(V) → Gr_k(V), the Grassmannian of all linear k-dimensional subspaces of V by defining p(U) to be the translation of U to a subspace through the origin. This projection is a fibration, and if V is given an inner product, the fibre containing U can be identified with $p(U)^{\perp }$ , the orthogonal complement to p(U). The fibres are therefore vector spaces, and the projection p is a vector bundle over the Grassmannian, which defines the manifold structure on Graff_k(V).

As a homogeneous space, the affine Grassmannian of an n-dimensional vector space V can be identified with

\mathrm {Graff} _{k}(V)\simeq {\frac {E(n)}{E(k)\times O(n-k)}}

where E(n) is the Euclidean group of Rⁿ and O(m) is the orthogonal group on R^m. It follows that the dimension is given by

\dim \left[\mathrm {Graff} _{k}(V)\right]=(n-k)(k+1)\,.

(This relation is easier to deduce from the identification of next section, as the difference between the number of coefficients, (n−k)(n+1) and the dimension of the linear group acting on the equations, (n−k)².)

Relationship with ordinary Grassmannian

Let (x₁,...,x_n) be the usual linear coordinates on Rⁿ. Then Rⁿ is embedded into Rⁿ⁺¹ as the affine hyperplane x_n+1 = 1. The k-dimensional affine subspaces of Rⁿ are in one-to-one correspondence with the (k+1)-dimensional linear subspaces of Rⁿ⁺¹ that are in general position with respect to the plane x_n+1 = 1. Indeed, a k-dimensional affine subspace of Rⁿ is the locus of solutions of a rank n − k system of affine equations

{\begin{aligned}a_{11}x_{1}+\cdots +a_{1n}x_{n}&=a_{1,n+1}\\&\vdots &\\a_{n-k,1}x_{1}+\cdots +a_{n-k,n}x_{n}&=a_{n-k,n+1}.\end{aligned}}

These determine a rank n−k system of linear equations on Rⁿ⁺¹

{\begin{aligned}a_{11}x_{1}+\cdots +a_{1n}x_{n}&=a_{1,n+1}x_{n+1}\\&\vdots &\\a_{n-k,1}x_{1}+\cdots +a_{n-k,n}x_{n}&=a_{n-k,n+1}x_{n+1}.\end{aligned}}

whose solution is a (k + 1)-plane that, when intersected with x_n+1 = 1, is the original k-plane.

Because of this identification, Graff(k,n) is a Zariski open set in Gr(k + 1, n + 1).

Related Research Articles

Euclidean space is the fundamental space of classical geometry. Originally, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any nonnegative integer dimension, including the three-dimensional space and the Euclidean plane. It was introduced by the Ancient Greek mathematician Euclid of Alexandria, and the qualifier Euclidean is used to distinguish it from other spaces that were later discovered in physics and modern mathematics.

In mathematics, a set $B$ of vectors in a vector space $V$ is called a basis if every element of $V$ may be written in a unique way as a finite linear combination of elements of $B$ . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to $B$ . The elements of a basis are called basis vectors.

Simplex Multi-dimensional generalization of triangle

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given space.

In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspace is a vector space that is a subset of some larger vector space. A linear subspace is usually simply called a subspace when the context serves to distinguish it from other types of subspaces.

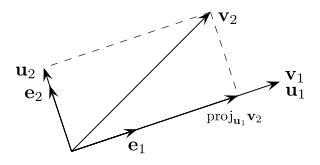
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalizing a set of vectors in an inner product space, most commonly the Euclidean space Rⁿ equipped with the standard inner product. The Gram–Schmidt process takes a finite, linearly independent set of vectors S = {v₁, …, v_k} for k ≤ n and generates an orthogonal set S′ = {u₁, …, u_k} that spans the same k-dimensional subspace of Rⁿ as S.

In linear algebra, the column space of a matrix A is the span of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.

In linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal vectors.

In mathematics, the orthogonal group in dimension $n$ , denoted $O(n)$ , is the group of distance-preserving transformations of a Euclidean space of dimension $n$ that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of $n \times n$ orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.

Projective space Completion of the usual space with "points at infinity"

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.

In mathematics, the Grassmannian $Gr (k, V)$ is a space that parameterizes all $k$ -dimensional linear subspaces of the $n$ -dimensional vector space $V$ . For example, the Grassmannian $Gr (1, V)$ is the space of lines through the origin in $V$ , so it is the same as the projective space of one dimension lower than $V$ .

In linear algebra and functional analysis, a projection is a linear transformation $from a vector space to itself such that . That is, whenever is applied twice to any value, it gives the same result as if it were applied once (idempotent). It leaves its image unchanged. Though abstract, this definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.$

In differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. Connections are among the simplest methods of defining differentiation of the sections of vector bundles.

In linear algebra, linear transformations can be represented by matrices. If $is a linear transformation mapping to and is a column vector with entries, then$

In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the linear subspace of the domain of the map which is mapped to the zero vector. That is, given a linear map $L : V \to W$ between two vector spaces $V$ and $W$ , the kernel of $L$ is the vector space of all elements $v$ of $V$ such that $L (v) = 0$ , where $0$ denotes the zero vector in $W$ , or more symbolically:

In mathematics, the Stiefel manifold $is the set of all orthonormal k -frames in That is, it is the set of ordered orthonormal k -tuples of vectors in It is named after Swiss mathematician Eduard Stiefel. Likewise one can define the complex Stiefel manifold of orthonormal k -frames in and the quaternionic Stiefel manifold of orthonormal k -frames in . More generally, the construction applies to any real, complex, or quaternionic inner product space.$

In mathematics, a real coordinate space of dimension $n$ , written $R n$ or $,$ is a coordinate space over the real numbers. This means that it is the set of the $n$ -tuples of real numbers. With component-wise addition and scalar multiplication, it is a real vector space.

In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert, in order to solve various counting problems of projective geometry. It was a precursor of several more modern theories, for example characteristic classes, and in particular its algorithmic aspects are still of current interest. The phrase "Schubert calculus" is sometimes used to mean the enumerative geometry of linear subspaces, roughly equivalent to describing the cohomology ring of Grassmannians, and sometimes used to mean the more general enumerative geometry of nonlinear varieties. Even more generally, “Schubert calculus” is often understood to encompass the study of analogous questions in generalized cohomology theories.

In mathematics, Hilbert spaces allow generalizing the methods of linear algebra and calculus from the two-dimensional and three dimensional Euclidean spaces to spaces that may have an infinite dimension. A Hilbert space is a vector space equipped with an inner product operation, which allows defining a distance function and perpendicularity. Furthermore, Hilbert spaces are complete for this distance, which means that there are enough limits in the space to allow the techniques of calculus to be used.

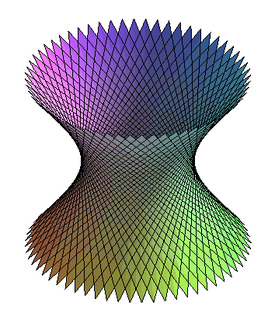
In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface

References

Klain, Daniel A.; Rota, Gian-Carlo (1997), Introduction to Geometric Probability, Cambridge: Cambridge University Press

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Affine Grassmannian (manifold)

Contents

Formal definition

Relationship with ordinary Grassmannian

Related Research Articles

References