Angela Kunoth

Last updated

Angela Kunoth (born 22 June 1963) [1] is a German mathematician specializing in the numerical analysis of partial differential equations. She is a professor of mathematics at the University of Cologne, [2] and the editor-in-chief of SIAM Journal on Numerical Analysis . [3]

Contents

Education and career

Kunoth studied mathematics at Bielefeld University beginning in 1982, and earned a diploma there in 1990. After visiting the University of South Carolina as a Fulbright Scholar, she completed a doctorate (Dr. rer. nat.) at the Free University of Berlin in 1994. [4] Her dissertation, Multilevel Preconditioning, was supervised by Wolfgang Dahmen. [5]

After research positions at SINTEF in Norway, at the Weierstrass Institute in Berlin, at Texas A&M University, and at RWTH Aachen University, she became an associate professor at the University of Bonn in 1999, and earned a habilitation through RWTH Aachen in 2000 with the habilitation thesis Wavelet Methods for Minimization Problems Involving Elliptic Partial Differential Equations. She moved to Paderborn University as a full professor and chair of complex systems in 2007, and at Paderborn served as director of the mathematical institute and vice-dean of the faculty for electrotechnics from 2010 to 2012. She moved again to the University of Cologne as professor and chair for applied mathematics in 2013. [4]

Kunoth was elected to the 2023 Class of SIAM Fellows. [6]

Book

Kunoth is the author of the monograph Wavelet Methods — Elliptic Boundary Value Problems and Control Problems (Springer, 2001), a book version of her habilitation thesis. [7]

Related Research Articles

Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).

In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.

Heinz-Otto Kreiss was a German mathematician in the fields of numerical analysis, applied mathematics, and what was the new area of computing in the early 1960s. Born in Hamburg, Germany, he earned his Ph.D. at Kungliga Tekniska Högskolan in 1959. Over the course of his long career, Kreiss wrote a number of books in addition to the purely academic journal articles he authored across several disciplines. He was professor at Uppsala University, California Institute of Technology and University of California, Los Angeles (UCLA). He was also a member of the Royal Swedish Academy of Sciences. At the time of his death, Kreiss was a Swedish citizen, living in Stockholm. He died in Stockholm in 2015, aged 85.

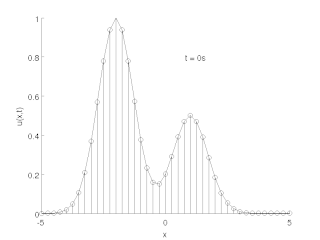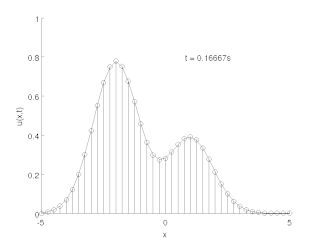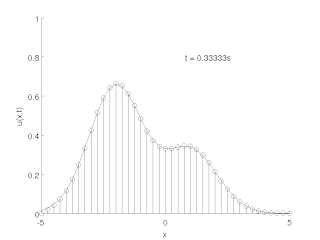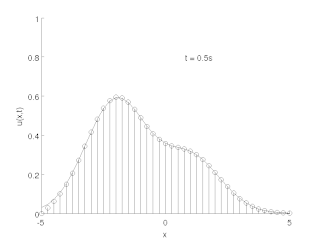
<span class="mw-page-title-main">Method of lines</span> Numerical method

The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. By reducing a PDE to a single continuous dimension, the method of lines allows solutions to be computed via methods and software developed for the numerical integration of ordinary differential equations (ODEs) and differential-algebraic systems of equations (DAEs). Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.

Christopher John Budd is a British mathematician known especially for his contribution to non-linear differential equations and their applications in industry. He is currently Professor of Applied Mathematics at the University of Bath, and was Professor of Geometry at Gresham College from 2016 to 2020.

<span class="mw-page-title-main">Randall J. LeVeque</span> American mathematician

Randall J. LeVeque is a Professor of Applied Mathematics at University of Washington who works in many fields including numerical analysis, computational fluid dynamics, and mathematical theory of conservation laws. Among other contributions, he is lead developer of the open source software project Clawpack for solving hyperbolic partial differential equations using the finite volume method. With Zhilin Li, he has also devised a numerical technique called the immersed interface method for solving problems with elastic boundaries or surface tension.

Burton Wendroff is an American applied mathematician known for his contributions to the development of numerical methods for the solution of hyperbolic partial differential equations. The Lax–Wendroff method for the solution of hyperbolic PDE is named for Wendroff.

<span class="mw-page-title-main">Ronald DeVore</span> American mathematician

Ronald Alvin DeVore is an American mathematician and academic. He is the Walter E. Koss Professor and a Distinguished Professor of Mathematics at Texas A&M University. DeVore is a member of the American Academy of Arts and Sciences and the National Academy of Sciences and a fellow of the American Mathematical Society.

<span class="mw-page-title-main">Wolfgang Dahmen</span> German mathematician

Wolfgang Dahmen is a German mathematician working in approximation theory, numerical analysis, and partial differential equations. In 2002, he was awarded the Gottfried Wilhelm Leibniz Prize and in 2011 the Gauss Lectureship. He was also a taekwondo athlete. He has been the Chair of the Society for the Foundations of Computational Mathematics (2014–).

The following is a timeline of numerical analysis after 1945, and deals with developments after the invention of the modern electronic computer, which began during Second World War. For a fuller history of the subject before this period, see timeline and history of mathematics.

<span class="mw-page-title-main">Harald Garcke</span> German mathematician

Harald Garcke is a German mathematician and professor at the University of Regensburg.

<span class="mw-page-title-main">Geneviève Raugel</span> French mathematician (1951–2019)

Geneviève Raugel was a French mathematician working in the field of numerical analysis and dynamical systems.

<span class="mw-page-title-main">Volker Mehrmann</span> German mathematician (born 1955)

Volker Ludwig Mehrmann is a German mathematician.

<span class="mw-page-title-main">Rolf Rannacher</span>

Rolf Rannacher is a German mathematician and a professor of numerical analysis at Heidelberg University.

Christoph Schwab is a German applied mathematician, specializing in numerical analysis of partial differential equations and boundary integral equations.

<span class="mw-page-title-main">Albert Cohen (mathematician)</span> French mathematician

Albert Cohen is a French mathematician, specializing in approximation theory, numerical analysis, and digital signal processing.

Karl Kunisch is an Austrian mathematician.

Monique Dauge is a French mathematician and numerical analyst specializing in partial differential equations, spectral theory, and applications to scientific computing. She is an emeritus senior researcher at the French National Centre for Scientific Research (CNRS), associated with the University of Rennes 1.

Rosemary Anne Renaut is a British and American computational mathematician whose research interests include inverse problems and regularization with applications to medical imaging and seismic analysis. She is a professor in the School of Mathematical and Statistical Sciences at Arizona State University.

Karl Edwin Gustafson is an American mathematician. Gustafson spent most of his career at the University of Colorado, Boulder, in the Department of Mathematics. He is known for developing the Antieigenvalue theory in applied mathematics.

References

  1. ↑ Birth date from Library of Congress catalog entry, retrieved 2020-05-27
  2. ↑ "Angela Kunoth, Prof. Dr.", Staff, University of Cologne, Department of Mathematics and Computer Science, Division of Mathematics, retrieved 2020-05-27
  3. ↑ "Editorial board", SIAM Journal on Numerical Analysis, SIAM, retrieved 2020-05-27
  4. 1 2 Short curriculum vitae , retrieved 2020-05-27
  5. ↑ Angela Kunoth at the Mathematics Genealogy Project
  6. ↑ "SIAM Announces Class of 2023 Fellows", SIAM News, SIAM, 30 March 2023, retrieved 2023-04-08
  7. ↑ Reviews of Wavelet Methods: Rémi Vaillancourt, Zbl   1011.65080; Peter G. Binev (2002), MR 1852351
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.