Related Research Articles

A generegulatory network (GRN) is a collection of molecular regulators that interact with each other and with other substances in the cell to govern the gene expression levels of mRNA and proteins which, in turn, determine the function of the cell. GRN also play a central role in morphogenesis, the creation of body structures, which in turn is central to evolutionary developmental biology (evo-devo).

Computer simulation is the process of mathematical modelling, performed on a computer, which is designed to predict the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determined by comparing their results to the real-world outcomes they aim to predict. Computer simulations have become a useful tool for the mathematical modeling of many natural systems in physics, astrophysics, climatology, chemistry, biology and manufacturing, as well as human systems in economics, psychology, social science, health care and engineering. Simulation of a system is represented as the running of the system's model. It can be used to explore and gain new insights into new technology and to estimate the performance of systems too complex for analytical solutions.

Cross-validation, sometimes called rotation estimation or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation includes resampling and sample splitting methods that use different portions of the data to test and train a model on different iterations. It is often used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. It can also be used to assess the quality of a fitted model and the stability of its parameters.
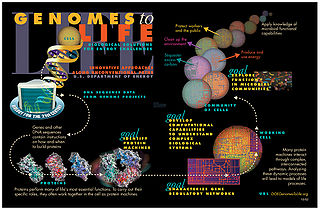
Systems biology is the computational and mathematical analysis and modeling of complex biological systems. It is a biology-based interdisciplinary field of study that focuses on complex interactions within biological systems, using a holistic approach to biological research.
Sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system can be divided and allocated to different sources of uncertainty in its inputs. A related practice is uncertainty analysis, which has a greater focus on uncertainty quantification and propagation of uncertainty; ideally, uncertainty and sensitivity analysis should be run in tandem.

An economic model is a theoretical construct representing economic processes by a set of variables and a set of logical and/or quantitative relationships between them. The economic model is a simplified, often mathematical, framework designed to illustrate complex processes. Frequently, economic models posit structural parameters. A model may have various exogenous variables, and those variables may change to create various responses by economic variables. Methodological uses of models include investigation, theorizing, and fitting theories to the world.
The fast Kalman filter (FKF), devised by Antti Lange (born 1941), is an extension of the Helmert–Wolf blocking (HWB) method from geodesy to safety-critical real-time applications of Kalman filtering (KF) such as GNSS navigation up to the centimeter-level of accuracy and satellite imaging of the Earth including atmospheric tomography.
A climate ensemble involves slightly different models of the climate system. The ensemble average is expected to perform better than individual model runs. There are at least five different types, to be described below.

Ensemble forecasting is a method used in or within numerical weather prediction. Instead of making a single forecast of the most likely weather, a set of forecasts is produced. This set of forecasts aims to give an indication of the range of possible future states of the atmosphere. Ensemble forecasting is a form of Monte Carlo analysis. The multiple simulations are conducted to account for the two usual sources of uncertainty in forecast models: (1) the errors introduced by the use of imperfect initial conditions, amplified by the chaotic nature of the evolution equations of the atmosphere, which is often referred to as sensitive dependence on initial conditions; and (2) errors introduced because of imperfections in the model formulation, such as the approximate mathematical methods to solve the equations. Ideally, the verified future atmospheric state should fall within the predicted ensemble spread, and the amount of spread should be related to the uncertainty (error) of the forecast. In general, this approach can be used to make probabilistic forecasts of any dynamical system, and not just for weather prediction.
Data assimilation is a mathematical discipline that seeks to optimally combine theory with observations. There may be a number of different goals sought – for example, to determine the optimal state estimate of a system, to determine initial conditions for a numerical forecast model, to interpolate sparse observation data using knowledge of the system being observed, to set numerical parameters based on training a model from observed data. Depending on the goal, different solution methods may be used. Data assimilation is distinguished from other forms of machine learning, image analysis, and statistical methods in that it utilizes a dynamical model of the system being analyzed.
Metabolic network modelling, also known as metabolic network reconstruction or metabolic pathway analysis, allows for an in-depth insight into the molecular mechanisms of a particular organism. In particular, these models correlate the genome with molecular physiology. A reconstruction breaks down metabolic pathways into their respective reactions and enzymes, and analyzes them within the perspective of the entire network. In simplified terms, a reconstruction collects all of the relevant metabolic information of an organism and compiles it in a mathematical model. Validation and analysis of reconstructions can allow identification of key features of metabolism such as growth yield, resource distribution, network robustness, and gene essentiality. This knowledge can then be applied to create novel biotechnology.

Local regression or local polynomial regression, also known as moving regression, is a generalization of the moving average and polynomial regression. Its most common methods, initially developed for scatterplot smoothing, are LOESS and LOWESS, both pronounced LOH-ess. They are two strongly related non-parametric regression methods that combine multiple regression models in a k-nearest-neighbor-based meta-model. In some fields, LOESS is known and commonly referred to as Savitzky–Golay filter.
Uncertainty quantification (UQ) is the science of quantitative characterization and estimation of uncertainties in both computational and real world applications. It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known. An example would be to predict the acceleration of a human body in a head-on crash with another car: even if the speed was exactly known, small differences in the manufacturing of individual cars, how tightly every bolt has been tightened, etc., will lead to different results that can only be predicted in a statistical sense.
Groundwater models are computer models of groundwater flow systems, and are used by hydrologists and hydrogeologists. Groundwater models are used to simulate and predict aquifer conditions.
Fluxomics describes the various approaches that seek to determine the rates of metabolic reactions within a biological entity. While metabolomics can provide instantaneous information on the metabolites in a biological sample, metabolism is a dynamic process. The significance of fluxomics is that metabolic fluxes determine the cellular phenotype. It has the added advantage of being based on the metabolome which has fewer components than the genome or proteome.

A hydrologic model is a simplification of a real-world system that aids in understanding, predicting, and managing water resources. Both the flow and quality of water are commonly studied using hydrologic models.
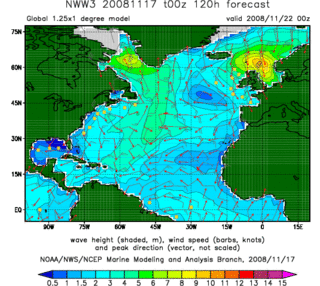
In fluid dynamics, wind wave modeling describes the effort to depict the sea state and predict the evolution of the energy of wind waves using numerical techniques. These simulations consider atmospheric wind forcing, nonlinear wave interactions, and frictional dissipation, and they output statistics describing wave heights, periods, and propagation directions for regional seas or global oceans. Such wave hindcasts and wave forecasts are extremely important for commercial interests on the high seas. For example, the shipping industry requires guidance for operational planning and tactical seakeeping purposes.

A cellular model is a mathematical model of aspects of a biological cell, for the purposes of in silico research.

Vflo is a commercially available, physics-based distributed hydrologic model generated by Vieux & Associates, Inc. Vflo uses radar rainfall data for hydrologic input to simulate distributed runoff. Vflo employs GIS maps for parameterization via a desktop interface. The model is suited for distributed hydrologic forecasting in post-analysis and in continuous operations. Vflo output is in the form of hydrographs at selected drainage network grids, as well as distributed runoff maps covering the watershed. Model applications include civil infrastructure operations and maintenance, stormwater prediction and emergency management, continuous and short-term surface water runoff, recharge estimation, soil moisture monitoring, land use planning, water quality monitoring, and water resources management.
System identification is a method of identifying or measuring the mathematical model of a system from measurements of the system inputs and outputs. The applications of system identification include any system where the inputs and outputs can be measured and include industrial processes, control systems, economic data, biology and the life sciences, medicine, social systems and many more.
References
- ↑ Hill, M.; Kavetski, D.; Clark, M.; Ye, M.; Arabi, M.; Lu, D.; Foglia, L.; Mehl, S. (2015). "Practical use of computationally frugal model analysis methods". Groundwater. 54 (2): 159–170. doi: 10.1111/gwat.12330 . OSTI 1286771. PMID 25810333.
- ↑ Hill, M.; Tiedeman, C. (2007). Effective Groundwater Model Calibration, with Analysis of Data, Sensitivities, Predictions, and Uncertainty. John Wiley & Sons.
- ↑ Selekman, JA; Das, A; Grundl, NJ; Palecek, SP (2013). "Improving efficiency of human pluripotent stem cell differentiation platforms using an integrated experimental and computational approach". Biotechnol Bioeng. 110 (11): 3024–37. doi:10.1002/bit.24968. PMC 3970199 . PMID 23740478.
- ↑ Tian, D; Solodin, NM; Rajbhandari, P; Bjorklund, K; Alarid, ET; Kreeger, PK (2015). "A kinetic model identifies phosphorylated estrogen receptor-α (ERα) as a critical regulator of ERα dynamics in breast cancer". FASEB J. 29 (5): 2022–31. doi: 10.1096/fj.14-265637 . PMC 4415015 . PMID 25648997.