In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x: where k is a positive constant.

In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.

In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that, in complex analysis, "differentiation is equivalent to integration": complex differentiation, like integration, behaves well under uniform limits – a result that does not hold in real analysis.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
In complex analysis, the Hardy spaces are spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz, who named them after G. H. Hardy, because of the paper. In real analysis Hardy spaces are spaces of distributions on the real n-space , defined as boundary values of the holomorphic functions. are related to the Lp spaces. For these Hardy spaces are subsets of spaces, while for the spaces have some undesirable properties, and the Hardy spaces are much better behaved. Hence, spaces can be considered extensions of spaces.

In mathematics, the Clausen function, introduced by Thomas Clausen, is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum, as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation for . The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi. Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later.
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and hypergeometric functions. It plays an important role in the theory of univalent functions, conformal mapping and Teichmüller spaces. It is named after the German mathematician Hermann Schwarz.
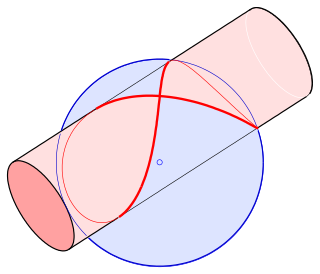
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z).

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
In mathematics, the ATS theorem is the theorem on the approximation of a trigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful.

In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.
In mathematics, singular integral operators of convolution type are the singular integral operators that arise on Rn and Tn through convolution by distributions; equivalently they are the singular integral operators that commute with translations. The classical examples in harmonic analysis are the harmonic conjugation operator on the circle, the Hilbert transform on the circle and the real line, the Beurling transform in the complex plane and the Riesz transforms in Euclidean space. The continuity of these operators on L2 is evident because the Fourier transform converts them into multiplication operators. Continuity on Lp spaces was first established by Marcel Riesz. The classical techniques include the use of Poisson integrals, interpolation theory and the Hardy–Littlewood maximal function. For more general operators, fundamental new techniques, introduced by Alberto Calderón and Antoni Zygmund in 1952, were developed by a number of authors to give general criteria for continuity on Lp spaces. This article explains the theory for the classical operators and sketches the subsequent general theory.
In mathematics, the Douady–Earle extension, named after Adrien Douady and Clifford Earle, is a way of extending homeomorphisms of the unit circle in the complex plane to homeomorphisms of the closed unit disk, such that the extension is a diffeomorphism of the open disk. The extension is analytic on the open disk. The extension has an important equivariance property: if the homeomorphism is composed on either side with a Möbius transformation preserving the unit circle the extension is also obtained by composition with the same Möbius transformation. If the homeomorphism is quasisymmetric, the diffeomorphism is quasiconformal. An extension for quasisymmetric homeomorphisms had previously been given by Lars Ahlfors and Arne Beurling; a different equivariant construction had been given in 1985 by Pekka Tukia. Equivariant extensions have important applications in Teichmüller theory; for example, they lead to a quick proof of the contractibility of the Teichmüller space of a Fuchsian group.
In mathematics, the Radó–Kneser–Choquet theorem, named after Tibor Radó, Hellmuth Kneser and Gustave Choquet, states that the Poisson integral of a homeomorphism of the unit circle is a harmonic diffeomorphism of the open unit disk. The result was stated as a problem by Radó and solved shortly afterwards by Kneser in 1926. Choquet, unaware of the work of Radó and Kneser, rediscovered the result with a different proof in 1945. Choquet also generalized the result to the Poisson integral of a homeomorphism from the unit circle to a simple Jordan curve bounding a convex region.
In mathematics, singular integral operators on closed curves arise in problems in analysis, in particular complex analysis and harmonic analysis. The two main singular integral operators, the Hilbert transform and the Cauchy transform, can be defined for any smooth Jordan curve in the complex plane and are related by a simple algebraic formula. In the special case of Fourier series for the unit circle, the operators become the classical Cauchy transform, the orthogonal projection onto Hardy space, and the Hilbert transform a real orthogonal linear complex structure. In general the Cauchy transform is a non-self-adjoint idempotent and the Hilbert transform a non-orthogonal complex structure. The range of the Cauchy transform is the Hardy space of the bounded region enclosed by the Jordan curve. The theory for the original curve can be deduced from that of the unit circle, where, because of rotational symmetry, both operators are classical singular integral operators of convolution type. The Hilbert transform satisfies the jump relations of Plemelj and Sokhotski, which express the original function as the difference between the boundary values of holomorphic functions on the region and its complement. Singular integral operators have been studied on various classes of functions, including Hölder spaces, Lp spaces and Sobolev spaces. In the case of L2 spaces—the case treated in detail below—other operators associated with the closed curve, such as the Szegő projection onto Hardy space and the Neumann–Poincaré operator, can be expressed in terms of the Cauchy transform and its adjoint.
Monin–Obukhov (M–O) similarity theory describes the non-dimensionalized mean flow and mean temperature in the surface layer under non-neutral conditions as a function of the dimensionless height parameter, named after Russian scientists A. S. Monin and A. M. Obukhov. Similarity theory is an empirical method that describes universal relationships between non-dimensionalized variables of fluids based on the Buckingham π theorem. Similarity theory is extensively used in boundary layer meteorology since relations in turbulent processes are not always resolvable from first principles.














