Minimal surface in differential geometry
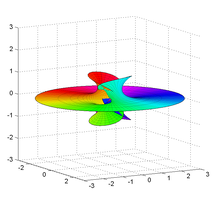
Richmond surface for m=2. In differential geometry , a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. [ 1] It is a family of surfaces with one planar end and one Enneper surface -like self-intersecting end.
It has Weierstrass–Enneper parameterization f ( z ) = 1 / z 2 , g ( z ) = z m {\displaystyle f(z)=1/z^{2},g(z)=z^{m}}
X ( z ) = ℜ [ ( − 1 / 2 z ) − z 2 m + 1 / ( 4 m + 2 ) ] Y ( z ) = ℜ [ ( − i / 2 z ) + i z 2 m + 1 / ( 4 m + 2 ) ] Z ( z ) = ℜ [ z m / m ] {\displaystyle {\begin{aligned}X(z)&=\Re [(-1/2z)-z^{2m+1}/(4m+2)]\\Y(z)&=\Re [(-i/2z)+iz^{2m+1}/(4m+2)]\\Z(z)&=\Re [z^{m}/m]\end{aligned}}} The associate family of the surface is just the surface rotated around the z-axis.
Taking m = 2 a real parametric expression becomes: [ 2]
X ( u , v ) = ( 1 / 3 ) u 3 − u v 2 + u u 2 + v 2 Y ( u , v ) = − u 2 v + ( 1 / 3 ) v 3 − v u 2 + v 2 Z ( u , v ) = 2 u {\displaystyle {\begin{aligned}X(u,v)&=(1/3)u^{3}-uv^{2}+{\frac {u}{u^{2}+v^{2}}}\\Y(u,v)&=-u^{2}v+(1/3)v^{3}-{\frac {v}{u^{2}+v^{2}}}\\Z(u,v)&=2u\end{aligned}}} This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.