
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which an atomic nucleus emits a beta particle, transforming into an isobar of that nuclide. For example, beta decay of a neutron transforms it into a proton by the emission of an electron accompanied by an antineutrino; or, conversely a proton is converted into a neutron by the emission of a positron with a neutrino in what is called positron emission. Neither the beta particle nor its associated (anti-)neutrino exist within the nucleus prior to beta decay, but are created in the decay process. By this process, unstable atoms obtain a more stable ratio of protons to neutrons. The probability of a nuclide decaying due to beta and other forms of decay is determined by its nuclear binding energy. The binding energies of all existing nuclides form what is called the nuclear band or valley of stability. For either electron or positron emission to be energetically possible, the energy release or Q value must be positive.

A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a nucleus of a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.

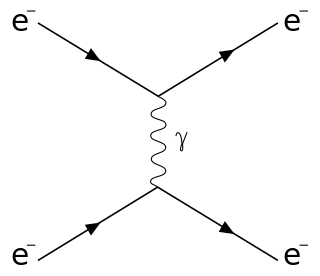
Compton scattering is the quantum theory of high frequency photons scattering following an interaction with a charged particle, usually an electron. Specifically, when the photon hits electrons, it releases loosely bound electrons from the outer valence shells of atoms or molecules.
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called diffuse reflections and unscattered reflections are called specular (mirror-like) reflections. Originally, the term was confined to light scattering. As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" in 1800. John Tyndall, a pioneer in light scattering research, noted the connection between light scattering and acoustic scattering in the 1870s. Near the end of the 19th century, the scattering of cathode rays and X-rays was observed and discussed. With the discovery of subatomic particles and the development of quantum theory in the 20th century, the sense of the term became broader as it was recognized that the same mathematical frameworks used in light scattering could be applied to many other phenomena.
In physics, mean free path is the average distance over which a moving particle travels before substantially changing its direction or energy, typically as a result of one or more successive collisions with other particles.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as where the vector r is the relative position between the charges. This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as 1/r2, the average number of particles at each distance r is proportional to r2, assuming the fluid is fairly isotropic. As a result, a charge fluctuation at any one point has non-negligible effects at large distances.
Electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either or . The density is determined, through definition, by the normalised -electron wavefunction which itself depends upon variables. Conversely, the density determines the wave function modulo up to a phase factor, providing the formal foundation of density functional theory.

Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of the structure of the material. The technique is similar to X-ray diffraction but due to their different scattering properties, neutrons and X-rays provide complementary information: X-Rays are suited for superficial analysis, strong x-rays from synchrotron radiation are suited for shallow depths or thin specimens, while neutrons having high penetration depth are suited for bulk samples.

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate electronic energy levels and the resulting splittings in those electronic energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.

In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude of torque the object experiences in a given magnetic field. When the same magnetic field is applied, objects with larger magnetic moments experience larger torques. The strength of this torque depends not only on the magnitude of the magnetic moment but also on its orientation relative to the direction of the magnetic field. Its direction points from the south pole to north pole of the magnet.

The reciprocal lattice is a term associated with solids with translational symmetry, and plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier transform of the lattice associated with the arrangement of the atoms. The direct lattice or real lattice is a periodic function in physical space, such as a crystal system. The reciprocal lattice exists in the mathematical space of spatial frequencies, known as reciprocal space or k space, which is the dual of physical space considered as a vector space, and the reciprocal lattice is the sublattice of that space that is dual to the direct lattice.

Neutron scattering, the irregular dispersal of free neutrons by matter, can refer to either the naturally occurring physical process itself or to the man-made experimental techniques that use the natural process for investigating materials. The natural/physical phenomenon is of elemental importance in nuclear engineering and the nuclear sciences. Regarding the experimental technique, understanding and manipulating neutron scattering is fundamental to the applications used in crystallography, physics, physical chemistry, biophysics, and materials research.
The Ewald sphere is a geometric construction used in electron, neutron, and x-ray diffraction which shows the relationship between:
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
The nuclear cross section of a nucleus is used to describe the probability that a nuclear reaction will occur. The concept of a nuclear cross section can be quantified physically in terms of "characteristic area" where a larger area means a larger probability of interaction. The standard unit for measuring a nuclear cross section is the barn, which is equal to 10−28 m2, 10−24 cm2 or 100 fm2. Cross sections can be measured for all possible interaction processes together, in which case they are called total cross sections, or for specific processes, distinguishing elastic scattering and inelastic scattering; of the latter, amongst neutron cross sections the absorption cross sections are of particular interest.
The Debye–Waller factor (DWF), named after Peter Debye and Ivar Waller, is used in condensed matter physics to describe the attenuation of x-ray scattering or coherent neutron scattering caused by thermal motion. It is also called the B factor, atomic B factor, or temperature factor. Often, "Debye–Waller factor" is used as a generic term that comprises the Lamb–Mössbauer factor of incoherent neutron scattering and Mössbauer spectroscopy.
In condensed matter physics and crystallography, the static structure factor is a mathematical description of how a material scatters incident radiation. The structure factor is a critical tool in the interpretation of scattering patterns obtained in X-ray, electron and neutron diffraction experiments.

X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. The resulting map of the directions of the X-rays far from the sample is called a diffraction pattern. It is different from X-ray crystallography which exploits X-ray diffraction to determine the arrangement of atoms in materials, and also has other components such as ways to map from experimental diffraction measurements to the positions of atoms.
In condensed matter physics, the dynamic structure factor is a mathematical function that contains information about inter-particle correlations and their time evolution. It is a generalization of the structure factor that considers correlations in both space and time. Experimentally, it can be accessed most directly by inelastic neutron scattering or X-ray Raman scattering.
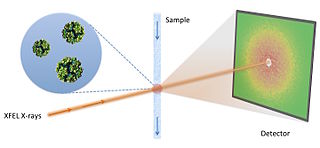
Fluctuation X-ray scattering (FXS) is an X-ray scattering technique similar to small-angle X-ray scattering (SAXS), but is performed using X-ray exposures below sample rotational diffusion times. This technique, ideally performed with an ultra-bright X-ray light source, such as a free electron laser, results in data containing significantly more information as compared to traditional scattering methods.






























