
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices, thus it is "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

In geometry, a five-dimensional polytope is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell.
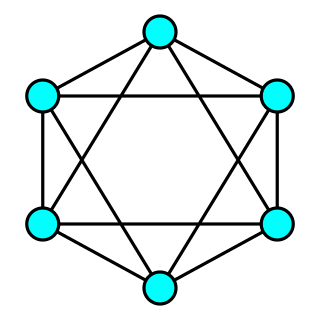
In graph theory, a connected graph G is said to be k-vertex-connected if it has more than k vertices and remains connected whenever fewer than k vertices are removed.

In mathematical programming and polyhedral combinatorics, the Hirsch conjecture is the statement that the edge-vertex graph of an n-facet polytope in d-dimensional Euclidean space has diameter no more than n − d. That is, any two vertices of the polytope must be connected to each other by a path of length at most n − d. The conjecture was first put forth in a letter by Warren M. Hirsch to George B. Dantzig in 1957 and was motivated by the analysis of the simplex method in linear programming, as the diameter of a polytope provides a lower bound on the number of steps needed by the simplex method. The conjecture is now known to be false in general.
In geometry, a vertex is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope P is another polyhedron or polytope PK formed by replacing each facet of P with a shallow pyramid. Kleetopes are named after Victor Klee.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.
In polyhedral combinatorics, a stacked polytope is a polytope formed from a simplex by repeatedly gluing another simplex onto one of its facets.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.
In mathematics, and more particularly in polyhedral combinatorics, Eberhard's theorem partially characterizes the multisets of polygons that can form the faces of simple convex polyhedra. It states that, for given numbers of triangles, quadrilaterals, pentagons, heptagons, and other polygons other than hexagons, there exists a convex polyhedron with those given numbers of faces of each type if and only if those numbers of polygons obey a linear equation derived from Euler's polyhedral formula.













