Bend minimization

Last updated

In graph drawing styles that represent the edges of a graph by polylines (sequences of line segments connected at bends), it is desirable to minimize the number of bends per edge (sometimes called the curve complexity) [1] or the total number of bends in a drawing. [2] Bend minimization is the algorithmic problem of finding a drawing that minimizes these quantities. [3] [4]

Contents

Eliminating all bends

The prototypical example of bend minimization is Fáry's theorem, which states that every planar graph can be drawn with no bends, that is, with all its edges drawn as straight line segments. [5]

Drawings of a graph in which the edges are both bendless and axis-aligned are sometimes called rectilinear drawings, and are one way of constructing RAC drawings in which all crossings are at right angles. [6] However, it is NP-complete to determine whether a planar graph has a planar rectilinear drawing, [7] and NP-complete to determine whether an arbitrary graph has a rectilinear drawing that allows crossings. [6]

Bend minimization

Tamassia (1987) showed that bend minimization of orthogonal drawings of planar graphs, in which the vertices are placed in an integer lattice and the edges are drawn as axis-aligned polylines, could be performed in polynomial time by translating the problem into one of minimum-cost network flow. [8] [9] However, if the planar embedding of the graph may be changed, then bend minimization becomes NP-complete, and must instead be solved by techniques such as integer programming that do not guarantee both a fast runtime and an exact answer. [10]

Few bends per edge

Many graph drawing styles allow bends, but only in a limited way: the curve complexity of these drawings (the maximum number of bends per edge) is bounded by some fixed constant. Allowing this constant to grow larger can be used to improve other aspects of the drawing, such as its area. [1] Alternatively, in some cases, a drawing style may only be possible when bends are allowed; for instance, not every graph has a RAC drawing (a drawing with all crossings at right angles) with no bends, or with curve complexity two, but every graph has such a drawing with curve complexity three. [11]

Related Research Articles

Graph drawing Visualization of node-link graphs

Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.

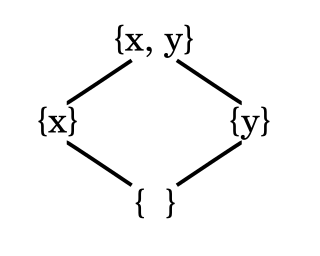
Hasse diagram Visual depiction of a partially ordered set

In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set (S, ≤) one represents each element of S as a vertex in the plane and draws a line segment or curve that goes upward from x to y whenever y covers x . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.

Book embedding Graph layout on multiple half-planes

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings into a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

Graph embedding Embedding a graph in a topological space, often Euclidean

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

Polygonal chain

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.

Crossing number (graph theory) Fewest edge crossings in drawing of a graph

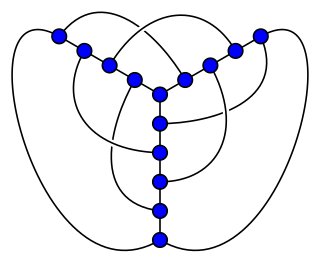
In graph theory, the crossing numbercr(G) of a graph G is the lowest number of edge crossings of a plane drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing.

Layered graph drawing Graph drawing with vertices in horizontal layers

Layered graph drawing or hierarchical graph drawing is a type of graph drawing in which the vertices of a directed graph are drawn in horizontal rows or layers with the edges generally directed downwards. It is also known as Sugiyama-style graph drawing after Kozo Sugiyama, who first developed this drawing style.

Angular resolution (graph drawing) Sharpest angle between edges at a vertex

In graph drawing, the angular resolution of a drawing of a graph is the sharpest angle formed by any two edges that meet at a common vertex of the drawing.

Slope number Number of edge slopes in graph drawing

In graph drawing and geometric graph theory, the slope number of a graph is the minimum possible number of distinct slopes of edges in a drawing of the graph in which vertices are represented as points in the Euclidean plane and edges are represented as line segments that do not pass through any non-incident vertex.

1-planar graph

In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.

In graph drawing, a universal point set of order n is a set S of points in the Euclidean plane with the property that every n-vertex planar graph has a straight-line drawing in which the vertices are all placed at points of S.

Circular layout Graph drawing with vertices on a circle

In graph drawing, a circular layout is a style of drawing that places the vertices of a graph on a circle, often evenly spaced so that they form the vertices of a regular polygon.

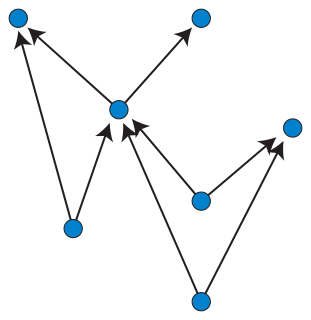
Upward planar drawing Graph with edges non-crossing and upward

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.

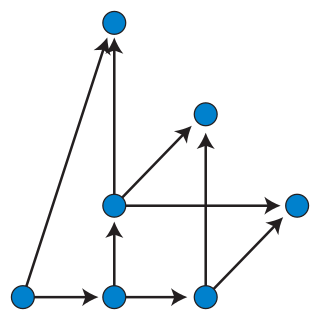
Dominance drawing Graph where coordinates show reachability

Dominance drawing is a style of graph drawing of directed acyclic graphs that makes the reachability relations between vertices visually apparent. In dominance drawing, vertices are placed at distinct points of the Euclidean plane and a vertex v is reachable from another vertex u if and only if both Cartesian coordinates of v are greater than or equal to the coordinates of u. The edges of a dominance drawing may be drawn either as straight line segments, or, in some cases, as polygonal chains.

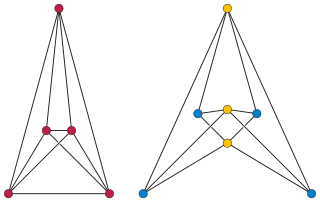
RAC drawing

In graph drawing, a RAC drawing of a graph is a drawing in which the vertices are represented as points, the edges are represented as straight line segments or polylines, at most two edges cross at any point, and when two edges cross they do so at right angles to each other. In the name of this drawing style, "RAC" stands for "right angle crossing".

In the mathematical field of graph theory, planarization is a method of extending graph drawing methods from planar graphs to graphs that are not planar, by embedding the non-planar graphs within a larger planar graph.

In graph drawing, the area used by a drawing is a commonly used way of measuring its quality.

Simultaneous embedding is a technique in graph drawing and information visualization for visualizing two or more different graphs on the same or overlapping sets of labeled vertices, while avoiding crossings within both graphs. Crossings between an edge of one graph and an edge of the other graph are allowed.

References

  1. 1 2 Di Giacomo, Emilio; Didimo, Walter; Liotta, Giuseppe; Meijer, Henk (2011), "Area, curve complexity, and crossing resolution of non-planar graph drawings", Theory of Computing Systems, 49 (3): 565–575, doi:10.1007/s00224-010-9275-6, MR   2822838 .
  2. ↑ Di Battista, Giuseppe; Eades, Peter; Tamassia, Roberto; Tollis, Ioannis G. (1998), Graph Drawing: Algorithms for the Visualization of Graphs (1st ed.), Prentice Hall, pp. 15–16, ISBN   978-0133016154 .
  3. ↑ Di Battista et al. (1998), p. 145.
  4. ↑ Purchase, Helen (1997), "Which aesthetic has the greatest effect on human understanding?", Graph Drawing: 5th International Symposium, GD '97 Rome, Italy, September 18–20, 1997, Proceedings, Lecture Notes in Computer Science, vol. 1353, pp. 248–261, doi: 10.1007/3-540-63938-1_67 , ISBN   978-3-540-63938-1 .
  5. ↑ Di Battista et al. (1998), p. 140.
  6. 1 2 Eades, Peter; Hong, Seok-Hee; Poon, Sheung-Hung (2010), "On rectilinear drawing of graphs", Graph Drawing: 17th International Symposium, GD 2009, Chicago, IL, USA, September 22-25, 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, Springer, pp. 232–243, doi: 10.1007/978-3-642-11805-0_23 , ISBN   978-3-642-11804-3, MR   2680455 .
  7. ↑ Garg, Ashim; Tamassia, Roberto (2001), "On the computational complexity of upward and rectilinear planarity testing", SIAM Journal on Computing , 31 (2): 601–625, doi:10.1137/S0097539794277123, MR   1861292 .
  8. ↑ Tamassia, Roberto (1987), "On embedding a graph in the grid with the minimum number of bends", SIAM Journal on Computing , 16 (3): 421–444, doi:10.1137/0216030, MR   0889400 .
  9. ↑ Cornelsen, Sabine; Karrenbauer, Andreas (2012), "Accelerated bend minimization", Journal of Graph Algorithms and Applications, 16 (3): 635–650, doi: 10.7155/jgaa.00265 , MR   2983428 .
  10. ↑ Mutzel, Petra; Weiskircher, René (2002), "Bend minimization in orthogonal drawings using integer programming", Computing and Combinatorics: 8th Annual International Conference, COCOON 2002, Singapore, August 15–17, 2002, Proceedings, Lecture Notes in Computer Science, vol. 2387, pp. 484–493, CiteSeerX   10.1.1.138.1513 , doi:10.1007/3-540-45655-4_52, ISBN   978-3-540-43996-7 .
  11. ↑ Didimo, Walter; Eades, Peter; Liotta, Giuseppe (2009), "Drawing graphs with right angle crossings", Algorithms and Data Structures: 11th International Symposium, WADS 2009, Banff, Canada, August 21-23, 2009. Proceedings, Lecture Notes in Computer Science, vol. 5664, pp. 206–217, doi:10.1007/978-3-642-03367-4_19, ISBN   978-3-642-03366-7 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.